working_helen
[R로 하는 통계분석] Classification 모델 적합과 평가 본문
1. Logistic regression
2. LDA
3. QDA
4. Naive Bayes model
5. classification model evaluation
1. Logistic Regression
: Binary Classification 반응변수 Y의 class가 0 또는 1


- q = P(Y=1) = E(Y)
f(q) = logit(q) = log(q/(1- q)) = log(odds ratio) = Xβ
- 주어진 x에 대한 결과 Y가 1이 될 확률의 예측값을 계산
예측된 확률에 적절한 threshold를 사용해 0 또는 1로 분류 (보통 0.5를 threshold로 사용)
- β = logit(P(Y=1))의 변화량 = log(odds ratio)의 변화량
exp(β) = odds ratio 변화량 = P(Y=1) / P(Y=0) 변화량
: 설명변수가 1단위 증가할 때 odds ratio가 exp(β)배 증가
- βj > 0 : xj가 증가하면 log(오즈비)가 증가 = P(Y=1)이 증가 = Y와 xj는 양의 관계

- 일반적인 Regression의 경우 LSE, MLE 등을 통해 β 추정
- Logistic Regression에선 n개의 관측값들의 average cross entropy loss로 β 추정
average cross entropy loss를 최소로 만드는 β
[R 코드]
ISLR2 패키지의 Default 데이터셋 사용
- X : balance(카드 잔액), income(연간 소득)
- Y : default(카드지불 불이행 여부)
방법 1 : `glm` 패키지 이용
lr.m1 = glm(default ~ balance + income, family = binomial, data = Default)
summary(lr.m1)
# 각 class에 속할 확률 : fitted.value
lr.m1$fitted.value[1:5]
# 예측 class : 확률의 threshold를 정해서 classification
pred1 = ifelse(lr.m1$fitted.values > 0.5, "Yes", "No")
pred1[1:5]
# Confusion Matrix 생성
table_lr1 = table(real = Default$default, pred = pred1)
table_lr1
- 방법 2 : `tidymodels` 패키지의 `logistic_reg` 함수 이용
lr.m2 <- logistic_reg(mode = "classification") %>%
set_engine("glm") %>%
fit(default ~ balance + income, data=Default)
lr.m2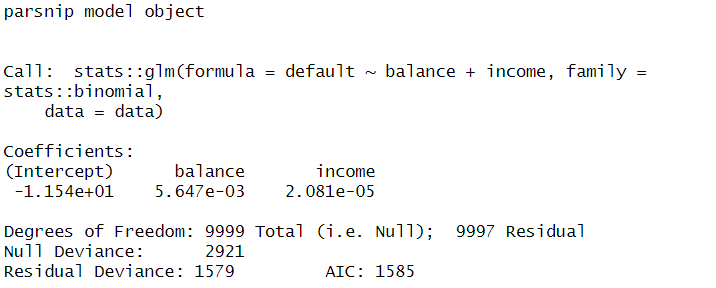
# type="class" : 0.5를 threshold로 classification
pred2 = predict(lr.m2, Default, type="class")$.pred_class
# type="prob" : 각 class에 속할 확률값, 직접 threshold를 정해서 classification
predict(lr.m2, Default, type="prob")
pred2 = ifelse(predict(lr.m2, Default, type="prob")$.pred_Yes > 0.5, "Yes", "No")
# Confusion Matrix 생성
table_lr2 = table(real = Default$default, pred = pred2)
table_lr2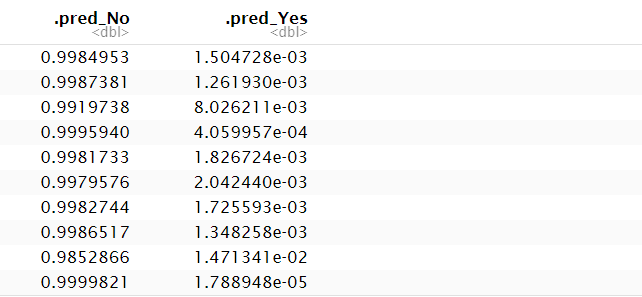
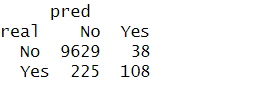
2. LDA (Linear Discriminant Analysis)
: Multiclass Classification 반응변수 Y의 class가 j = 1, 2, ... k
LDA의 가정 : P(x|Y=j) ~ N(μ_j, Σ)
- Y=j class에서 x의 조건부 분포(likelihood)가 multivariate normal(Gausian) distribution을 따른다
- Y=j에 따라 평균 μ_j는 다르지만, 공분산 행렬 Σ는 동일하다
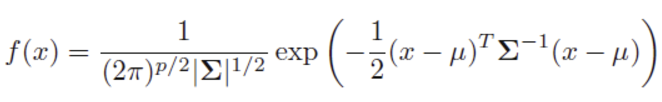
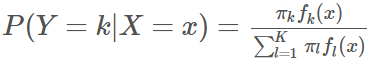
- 베이즈 정리를 이용해 사후확률 P(Y=j | x) = P_j(x)를 계산
사후확률을 최대로 만드는 class로 분류
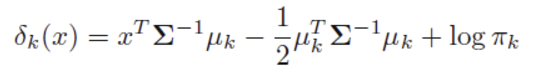
- 판별 함수를 최소화하는 class j로 분류
- Y를 어떤 class로 분류할지 결정하는 최종 판별 함수의 형태가 x에 대한 선형함수이기 때문에 'Linear'라는 이름이 사용됨
[R 코드]
lda.m = lda(default ~ balance + income, data = Default)
lda.m
# $class : 0.5를 threshold로 예측된 classes
predict(lda.m)$class[1:5]
# $posterior : 각 class에 속할 확률
predict(lda.m)$posterior[1:5,]
# Confusion Matrix 생성
table_lda = table(real = Default$default, pred = predict(lda.m)$class)
table_lda
3. QDA (Quadratic Discriminant Analysis)
: Multiclass Classification 반응변수 Y의 class가 j = 1, 2, ... k
QDA의 가정 : P(x|Y=j) ~ N(μ_j, Σ_j)
- Y=j class에서 x의 조건부 분포(likelihood)가 multivariate normal(Gausian) distribution을 따른다
- Y=j에 따라 서로 다른 평균 μ_j와 공분산 행렬 Σ_j를 가진다
- LDA와 달리 QDA는 각 class마다 서로 다른 공분산 행렬을 갖는다고 가정
- LDA와 동일하게 베이즈 정리를 통해 사후 확률을 계산한 후 이를 최대화하는 class로 분류
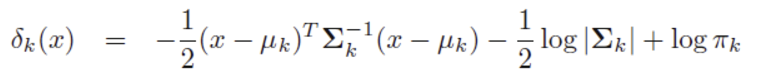
- 판별 함수를 최소화하는 class j로 분류
- 즉 Y를 어떤 class로 분류할지 결정하는 최종 판별 함수의 형태가 x에 대한 이차식함수이기 때문에 'Quadratic'라는 이름이 사용
- LDA vs QDA
- LDA는 동일한 공분산 행렬을 사용하기 때문에 모델 적합 시 QDA보다 더 적은 파라미터를 가짐, variance가 더 작음
- QDA는 LDA보다 더 많은 파라미터를 사용해 더 flexible한 모델, bias가 더 작음
- train data 수가 작아 vaiance를 줄이는 것이 중요한 경우 LDA 사용이 더 적합
- LDA의 등분산 가정이 적합하지 않은 경우 QDA 사용이 더 적합
[R 코드]
qda.m = qda(default ~ balance + income, data = Default)
qda.m
# $class : 0.5를 threshold로 예측된 classes
predict(qda.m)$class[1:5]
# $posterior : 각 class에 속할 확률
predict(qda.m)$posterior[1:5,]
# Confusion Matrix 생성
table_qda = table(real = Default$default, pred = predict(qda.m)$class)
table_qda
4. Naive Bayes
Naive Bayes의 개념
2024.03.17 - [교내 수업/Machine Learning] - [ Week 2-2 ] Naive Bayes Model
[ Week 2-2 ] Naive Bayes Model
Lecture : Machine LearningDate : week 2, 2024/03/07Topic : Naive Bayes Model 1. Bayes' Rule2. Naive Bayes Model 1) Model's Assumption 2) Model's Prediction 3) Smoothing 4) 장단점3. Naive Bayes Model 예제 1. Bayes' Rule (베이
working-helen.tistory.com
[R 코드]
- A-priori probabilities: 사전확률, P(Y=class)
- Conditional probabilities table: 가능도, P(X|Y=class)
nb.m = naiveBayes(default ~ balance + income, data = Default)
nb.m
# 각 Coditional probabilities table에서
# 1열 = 각 class에서의 mean(X), 2열 = 각 class에서의 sd(X)
# Y=No에서 balance의 mean이 803.9438, sd가 456.4762이라는 의미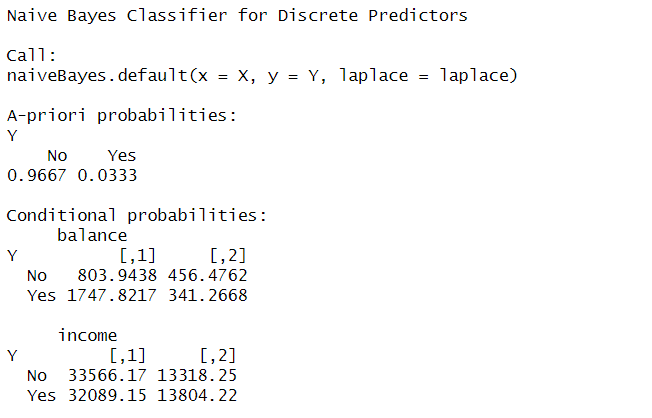
# type = "class" : 0.5를 threshold로 예측된 classes
predict(nb.m, Default, type="class")[1:5]
# type = "raw" : 각 class에 속할 확률
predict(nb.m, Default, type = "raw")[1:5]
# Confusion Matrix 생성
table_nb = table(real = Default$default, pred = predict(nb.m, Default))
table_nb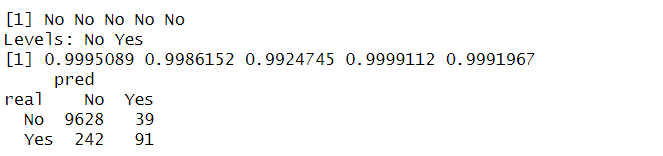
5. classification model evaluation
1) confusion matrix
→ accuracy / precision / recall = sensitivity / specificity / f1 score
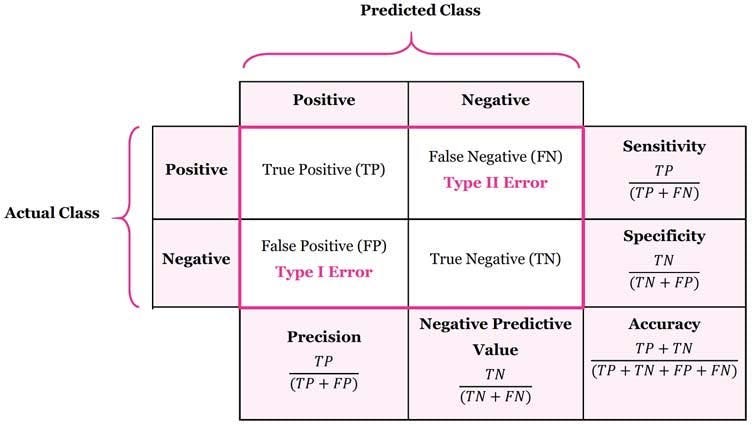
| 평가 지표 | 정의 | 성능 평가 |
| accuracy | 예측 결과 정답인 비율 | - accuracy값이 높을수록 모델 성능이 좋음 - 가장 일반적으로 사용되는 지표 - class 간 불균형이 심한 데이터인 경우 적절한 평가 지표가 되지 못함 |
| precision | 모델이 True라고 분류한 것 중에서 실제로 True인 것의 비율 | - precision이 낮아 모델이 정확하지 않을수록 negative이지만 positive로 예측하는 FP가 증가 |
| recall = sensitivity |
실제 True인 것 중에서 모델이 True라고 예측한 것의 비율 | - recall(sensitivity)이 낮으면 데이터에서 positive case들을 잘 찾지 못해 TP가 감소하고 FN이 증가 |
| specificity | 실제 False인 것 중에서 모델이 False라고 예측한 것의 비율 | - specificity가 낮으면 데이터에서 negative case들을 잘 찾지 못해 TN가 감소하고 FP가 증가 |
| f1 score | precision과 recall의 조화평균 (precision과 recall의 중요성을 동등하게 가정) |
- precision과 recall이 모두 높을수록 높아지며 1에 가까울수록 성능이 좋음 (0~1의 값) - f1 score은 불균형 데이터에도 적용할 수 있어 accuracy의 대체 평가지표로 사용 |
[R코드]
방법 1 : 각 metircs의 정의를 기반으로 manually 계산
# 2*2 행렬에서 evaluation metrics 계산 함수
accu <- function(table){(table[1,1]+table[2,2])/sum(table)}
sens <- function(table){(table[2,2])/(table[2,1]+table[2,2])}
spec <- function(table){(table[1,1])/(table[1,1]+table[1,2])}
prec <- function(table){(table[2,2])/(table[1,2]+table[2,2])}
f1 <- function(table){
sensitivity = sens(table)
precision = prec(table)
return(2*sensitivity*precision/(sensitivity+precision))
}
accu(table_lr2); sens(table_lr2); spec(table_lr2); prec(table_lr2); f1(table_lr2)
방법 2 : `caret` 패키지 사용
- confusionMatrix( predicted class, true class, positive )
- positive = "Yes" : positive로 인식할 항목을 지정, 별도로 지정하지 않으면 알파벳 순서가 처음인 class를 positive로 인식
- 예측값과 실제값 입력시 factor 형태로 전달해야하기 때문에 as.factor 사용
pred <- ifelse(lr.m2$fitted.values > 0.5, "Yes", "No")
confusionMatrix(as.factor(pred), Default$default, positive = "Yes")
- confusionMatrix( t(Confusion Matrix), positive )
- confusion matrix를 입력, 이때 예측값을 row 사용하기 때문에 confusion matrix 를 transpose한 형태로 입력
- 위 코드와 아래 코드 모두 동일한 결과
confusionMatrix(t(table_lr2), positive = "Yes")
conf_mat_lr = confusionMatrix(t(table_lr2), positive = "Yes")
conf_mat_lr$table # Confusion Matrix
conf_mat_lr$positive # positive class의 라벨
conf_mat_lr$byClass # evaluation metrics 값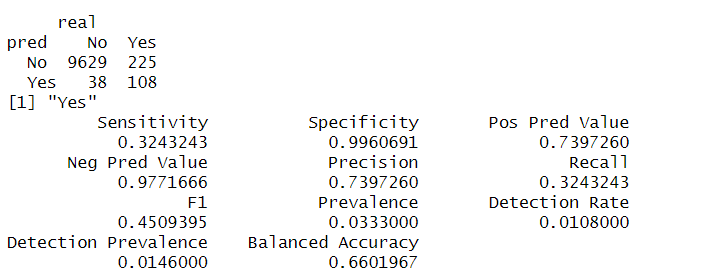
방법 3 : metrics_vec() 함수로 구하기
- 예측값과 실제값 입력시 factor 형태로 전달해야하기 때문에 as.factor 사용
- event_level = "second" : classes 중에서 positive로 인식할 class를 지정, 별도로 지정하지 않으면 실제값 factor의 첫번재 class를 positive로 간주
- 이 예시에서는 `default`의 `second` class에 해당하는 "Yes"를 positive로 인식하도록 지정
pred <- ifelse(lr.m1$fitted.values > 0.5, "Yes", "No")
accuracy_vec(Default$default, as.factor(pred))
sens_vec(Default$default, as.factor(pred), event_level = "second")
spec_vec(Default$default, as.factor(pred), event_level = "second")
precision_vec(Default$default, as.factor(pred), event_level = "second")
2) ROC curve와 AUC
: classification 모델의 threshold를 결정해야하는 경우 사용
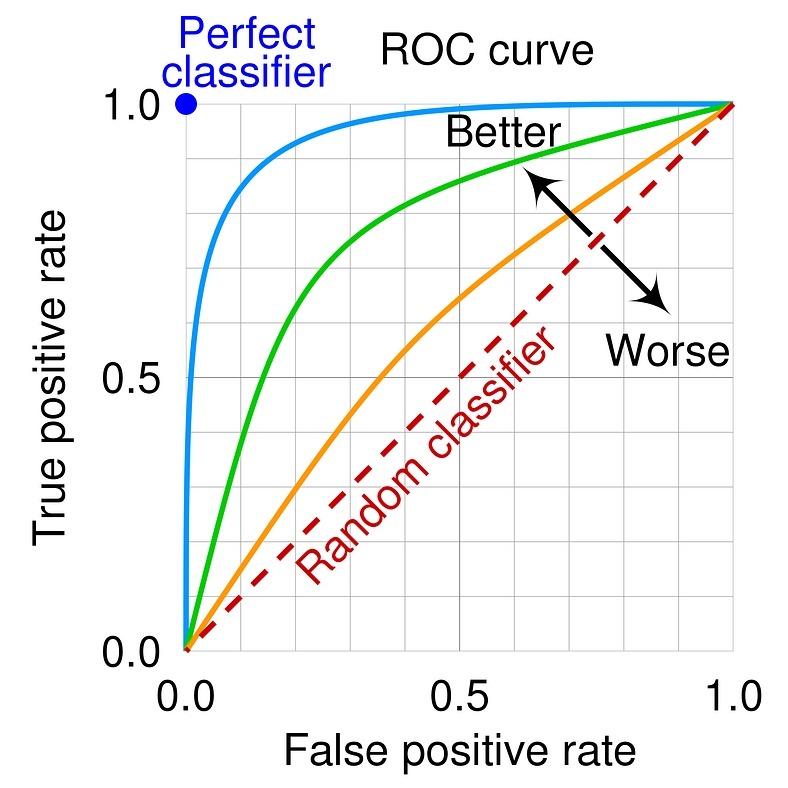
- 각 threshold 값에서의 (FPR, TPR) 값을 시각화
- x축 = 1- specificity = False Positive Rate(FPR)
- y축 = sensitivity = True Positive Rate(TPR)
- AUC = ROC 커브 아래의 면적을 계산한 값
- ROC 커브가 좌상단에 가까울수록 = FPR은 낮고 TPR이 높을수록 = AUC값이 높을수록
더 성능이 좋은 classification 모델이라고 할 수 있음
[R 코드]
- roc용 데이터프레임 생성 : 각 classes로의 예측값 + 실제값 정보가 모두 포함된 dataframe 생성
predictions <- predict(lr.m2, Default, type = "prob") %>%
bind_cols(Default %>% select(default))
predictions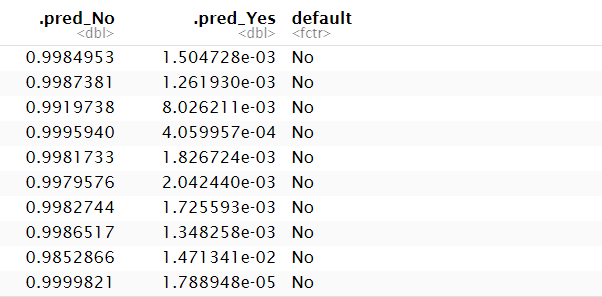
- ROC curve 그리기 : autoplot() 함수를 사용해 ROC curve 자동 생성
- data : 앞서 생성한 roc용 데이터프레임
- truth : 실제값 열 이름
- .pred_Yes : positive class의 예측값 열 이름
- event_level : positive로 사용할 class를 지정
roc_curve(data = predictions, truth = default, .pred_Yes, event_level = "second") %>%
autoplot()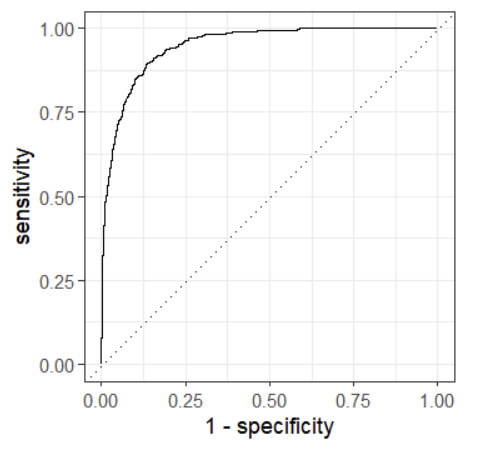
- AUC 값 계산
roc_auc(predictions, truth = default, .pred_Yes, event_level = "second")
Reference
https://wikidocs.net/32045
https://godongyoung.github.io/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D/2018/01/23/ISL-Classification_ch4.html
https://medium.com/@msong507/understanding-the-roc-auc-curve-cc204f0b3441
'교내 수업 > R 통계분석' 카테고리의 다른 글
| [R로 하는 통계분석] GAM(Generalized Additive Models) (0) | 2024.11.29 |
|---|---|
| [R로 하는 통계분석] Piecewise polynomial regression, Splines (0) | 2024.11.25 |
| [R로 하는 통계분석] Linear Regression feature selection (0) | 2024.11.09 |
| [R로 하는 통계분석] Linear Regression / GLM (0) | 2024.11.03 |
| [R로 하는 통계분석] Bootstrap 신뢰구간 추정 (0) | 2024.11.03 |




