working_helen
[R로 하는 통계분석] GAM(Generalized Additive Models) 본문
1. GAM (Generalized Additive Models)
2. GAM R 코드로 구현하기
1. GAM (Generalized Additive Models)
" 각 feature에 대한 비선형 함수를 선형결합 "
= 각각의 설명변수 xj에 대해선 비선형 함수 fj(xij)를 적합 + fj(xij)들을 선형결합

- 각 fj는 glm, spline, identity 등 단일변수로 y를 예측하는 어떠한 모델이든 사용 가능
- linear additivity 유지함으로써 fj를 단순히 선형결합하여 최종 모델 적합
GAM regression 모델링 예시
- `year` : natural spline, 자유도 4
- `age` : natural spline, 자유도 5
- `education` : step function

- logistic regression GAM
: prediction term을 linear Xβ 대신 GAM 모델 이용

GAM classification 모델링 예시
- `year` : linear function
- `age` : smoothing spline, 자유도 5
- `education` : step function

2. GAM R 코드로 구현하기
"ISLR2" 패키지 Wage 데이터셋 사용

다양한 fucntion을 사용해 GAM 모델 fitting
- `gam` : year에는 natural splines + age에는 smooth splines + education는 step function
- `gam1` : year, age에는 smooth splines + education는 step function
- `gam2` : age에는 smooth splines + education는 step function
- `gam3` : year에는 linear function + age에는 smooth splines + education는 step function
모델 해석
- Parametric Effects :
매개변수의 수가 고정된 모델의 효과에 대한 유의성 검정
natural spline은 매개변수 개수가 고정되어 있으므로 Parametric Effects로 검정 - Nonparametric Effects :
매개변수 수가 고정되어 있지 않고 학습 과정에서 결정되는 모델의 효과에 대한 유의성 검정
smooth spline은 regularization term lambda에 의해 최적화되기 때문에 Nonparametric Effects로 검정
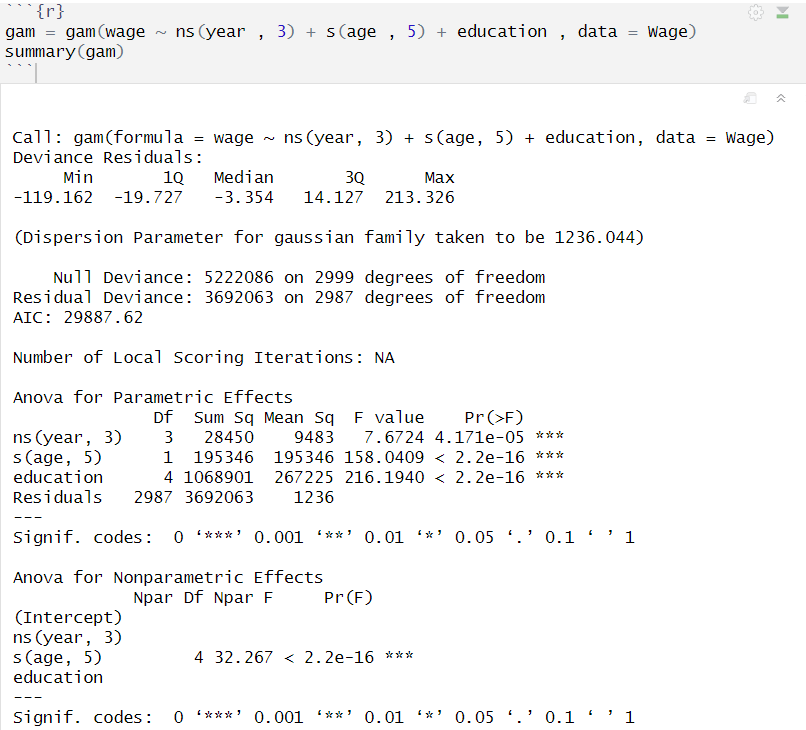
(1) `gam` fitting & 모델 해석
- `ns(feature, df)` : natural spline / `s(feature, df)` : smooth spline
- Anova for Parametric Effects :
`year` natural spline에서 유의미, `education` step function에서 유의미
`age`는 선형 관계에서 유의미
- Anova for Nonparametric Effects :
`age`는 smooth spline에서도 유의미
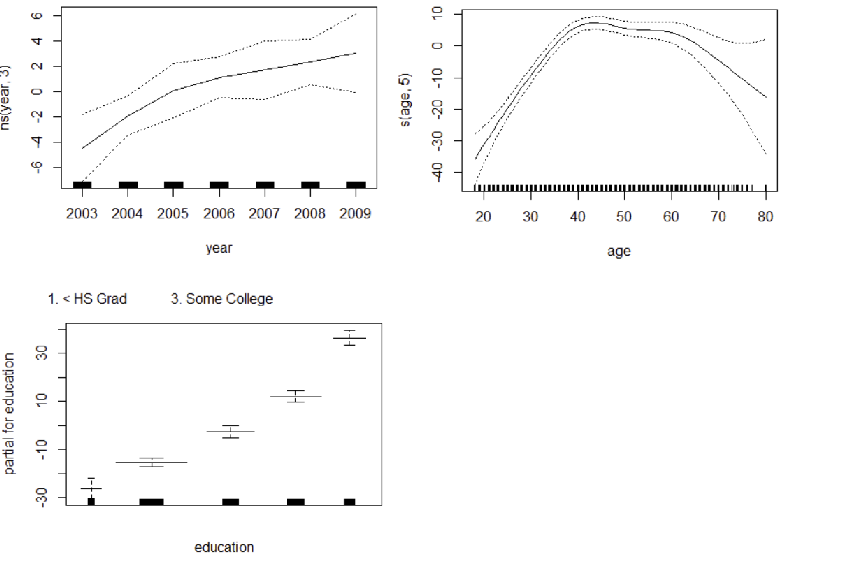
- 각 설명변수 function별 fitting 결과 시각화

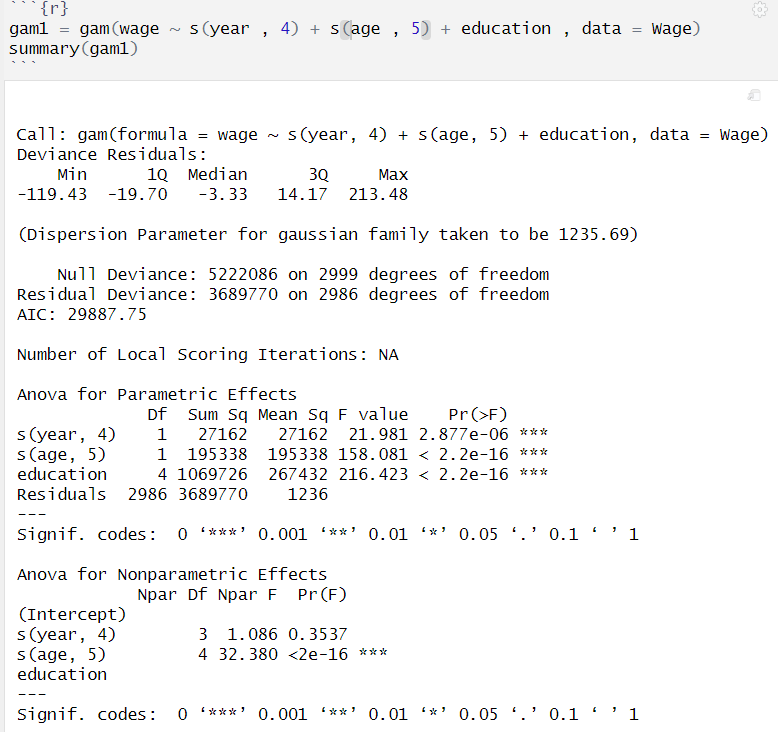
(2) `gam1` fitting & 모델 해석
- Anova for Parametric Effects :
`education` step function에서 유의미, `year`와 `age`는 선형관계에서 유의미
- Anova for Nonparametric Effects :
`year`는 비선형 관계에서 유의미하지 않음, `age`는 선형과 비선형 모두 유의미
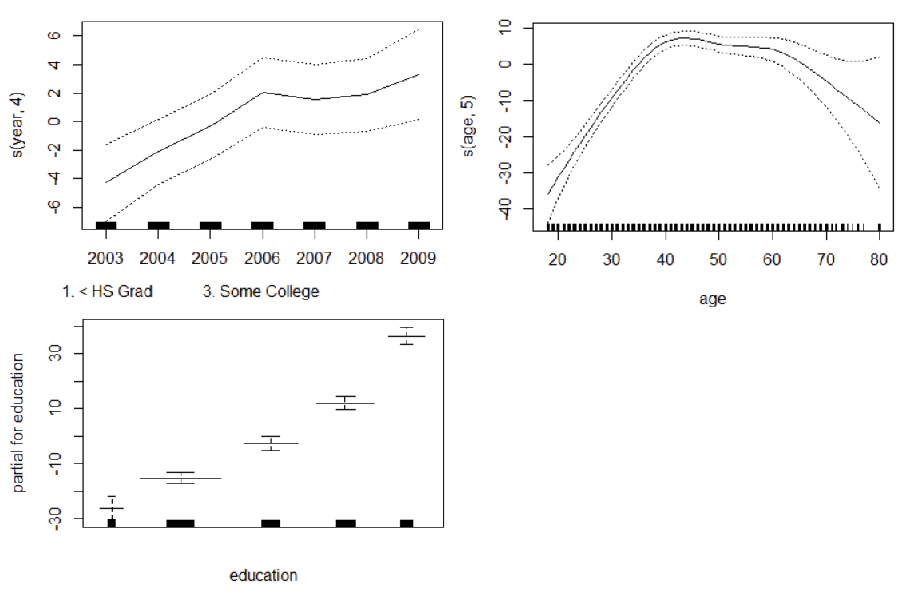
- 각 설명변수 function별 fitting 결과 시각화
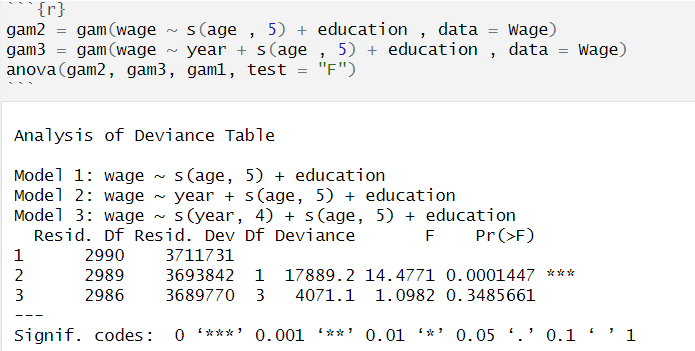
(2) `gam2`, `gam3` fitting & function 종류에 따른 모델 성능 비교
- `gam2` : `year`를 아예 설명변수로 사용하지 않은 모델
- `gam3` : `year`에 linear function를 사용한 경우 `gam2`에 비해 유의미하게 더 좋은 모델
- `gam1` : `year`에 smooth spline를 사용한 경우 `gam2`에 비해 좋지 않음
Reference
https://direction-f.tistory.com/97
본 포스팅은 James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning with Applications in R. Springer. 책을 참고하여 작성했습니다.
'교내 수업 > R 통계분석' 카테고리의 다른 글
| [R로 하는 통계분석] Piecewise polynomial regression, Splines (0) | 2024.11.25 |
|---|---|
| [R로 하는 통계분석] Classification 모델 적합과 평가 (0) | 2024.11.20 |
| [R로 하는 통계분석] Linear Regression feature selection (0) | 2024.11.09 |
| [R로 하는 통계분석] Linear Regression / GLM (0) | 2024.11.03 |
| [R로 하는 통계분석] Bootstrap 신뢰구간 추정 (0) | 2024.11.03 |





