working_helen
[R로 하는 통계분석] Linear Regression feature selection 본문
1. linear model fitting method
2. subset selection
3. subset selection R 코드로 구현하기
4. regularization
5. regularization R 코드로 구현하기
1. linear model fitting method

- p개의 설명변수 X, 반응변수 Y
- 기본적으로 linear model은 LSE(least square estimation) 방법으로 회귀계수 추정
- 관측치 수가 충분히 많지 않거나 설명변수가 너무 많은 경우,
설명변수를 너무 많이 포함하면 과적합이 일어나고 model complexity가 증가
- LSE 대신 다른 model fitting 방법을 사용
- subset selection : 전체 변수 중 일부만 사용하여 model fitting
- regularization : 설명변수 개수에 penalty를 부여하는 loss function 사용
- Y와 크게 관련없는 X들의 회귀계수 추정량을 제외하거나 제약을 둠으로써
① prediction ↑ : bias는 무시할만한 수준으로 증가시키면서 variance를 크게 감소시켜 모델 성능 개선
② interpretation ↑ : 관련없는 X들의 회귀계수를 0으로 만들어 모델을 더 간단하게 만듬
2. subset selection
: p개의 X들 중 Y의 변동성을 설명하기에 충분한 subset을 선택
- Best Subset selection : p개의 X로 만들 수 있는 모든 X subset에서 각각 모델을 적합한 후 RSS(SSE, L2 norm)가 최소가 되는 X subset을 선택
- Stepwise selection : 많은 계산량으로 인해 Best Subset selection을 사용하기 어려울 때, 단계적으로 모델에 사용할 X를 선택
- Forward Stepwise selection : X를 하나도 포함하지 않은 모델에서부터 모든 X를 다 포함하는 모델까지 X를 하나씩 추가하며 모델 적합, 각 단계에선 모델의 RSS를 최소로 만드는 X subset을 선택
- Backward Stepwise selection : 모든 X를 다 포함하는 모델에서부터 X를 하나도 포함하지 않는 모델까지 X를 하나씩 제거하며 모델 적합, 각 단계에선 모델의 RSS를 최소로 만드는 X subset을 선택
- hybrid approaches : forward와 유사하게 단계적으로 새로운 X를 추가하는 동시에, backward와 유사하게 새로운 모델에서 모델 성능을 개선시키지 않는 X들은 제거
3. subset selection R 코드로 구현하기
ISLR2 package의 Hitters 데이터
- 반응변수 Y = 'Salary'

Best Subset selection 수행 : regsubsets() 함수

- nvmax = 19 : X 최대 19개까지 포함
- "*" : 각 단계에서 모델에 포함된 변수 표시
예를 들어 변수 개수 1개일 땐 'CRBI', 2개일 땐 'CRBI'와 'Hits'가 선택

- id : 모델에 사용되는 변수 개수,
id 개수의 변수를 사용했을때 선택되는 변수의 종류 + 각 변수의 회귀계수 추정량 확인
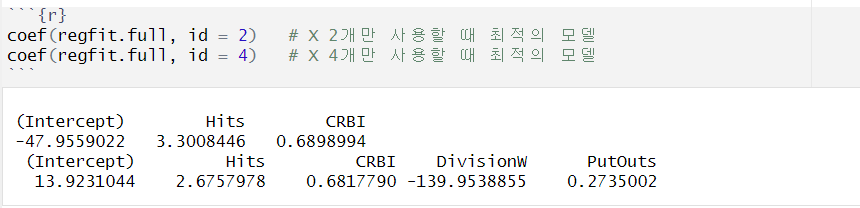
- model evaluation
- R2 : 설명변수 X를 추가할수록 항상 모델 성능이 좋아짐
- adjusted R2 : 값이 클수록 더 성능이 좋은 모델
- AIC : 값이 작을수록 더 성능이 좋은 모델
- BIC : 값이 작을수록 더 성능이 좋은 모델
- adjusted R2 기준, 변수 11개를 사용한 경우 최적의 모델
AIC 기준, 변수 10개를 사용한 경우 최적의 모델
BIC 기준, 변수 6개를 사용한 경우 최적의 모델


Forward Subset selection 수행 : regsubsets() 함수 + method = "forward"

Backward Subset selection 수행 : regsubsets() 함수 + method = "backward"

Subset selection 방식에 따른 결과 비교
- BIC 기준, best subset selection과 forward selection에선 6개의 변수를 사용한 모델이 가장 적절했고, backward selection에선 8개의 변수를 사용한 모델이 가장 적절

- 각각의 방법에서 최적의 변수 개수 사용시 선택된 X의 종류 및 회귀계수 추정량
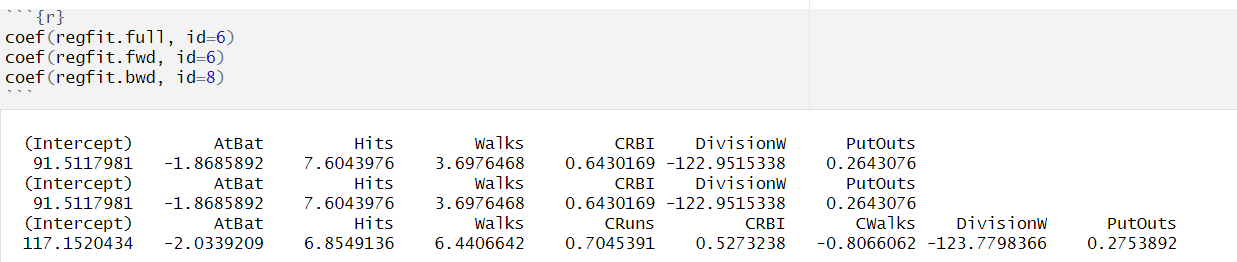
4. regularization
: loss function에 회귀계수 추정량이 너무 커지지 않도록 제어하는 penalty항 추가
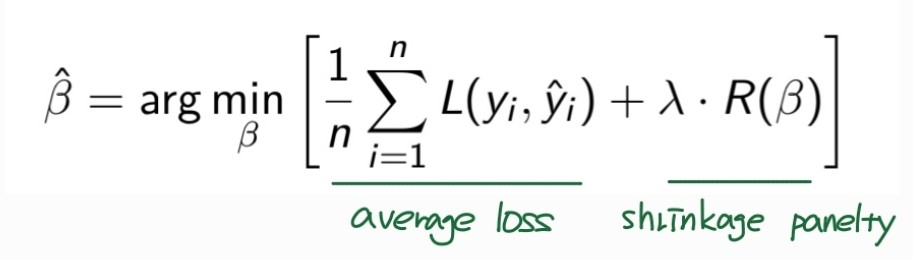
- λ : regularization hyperparameter
- λ = 0 : penalty를 주지 않는 경우, LSE와 동일한 결과
- λ 커질수록 X 개수에 더 강한 penalty 부여
- λ → ∞ : 거의 모든 X의 회귀계수 추정량이 0으로 수렴
- Rigde regression : L2 penalty 사용
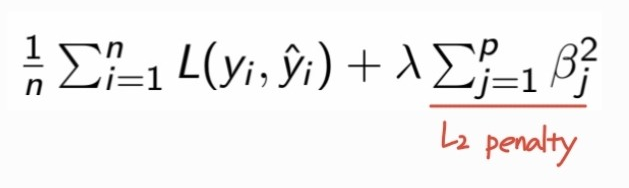
- Lasso regression : L1 penalty 사용
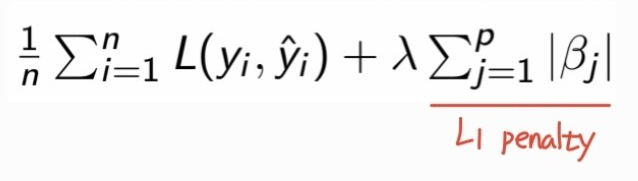
5. regularization R 코드로 구현하기
ISLR2 package의 Hitters 데이터
- 반응변수 Y = 'Salary'
- train-test split : 다양한 λ 값 중 최적의 모델 성능을 보이는 λ를 찾기 위해 train MSE와 test MSE 비교

lambda grid 설정
- ridge나 lasso 코드 내에서 lambda = grid로 실험하고 싶은 λ값 sequence를 지정 가능
- 별도로 지정하지 않으면 glmnet 함수는 자체적으로 λ값 sequence 를 생성해 모델 학습
- seq(10, -2, length = 100) : 10부터 -2까지 값을 가지는, 길이 100짜리 벡터

glmnet() 함수
- alpha : Ridge regression과 Lasso regression 중 panelty 종류 결정
- standardize : 설명변수 x 정규화 여부 결정
✏️ Ridge와 Lasso에서 standardization이 중요한 이유!
: 두 방법 모두 회귀계수의 크기를 기반으로 한 panelty를 사용하고 있다. 이때 각 설명변수 x마다 scale이 서로 다르면 예측 회귀계수의 scale도 달라지고, 규제항에서 각 변수별로 영향을 받는 정도도 달라진다. 따라서 모든 설명변수의 scale을 동일하게 만들어주는 standarization(정규화)를 통해 특정 설명변수가 scale 차이로 인해 규제항에 더 많은 영향을 미쳐 결과가 왜곡되는 것을 막을 수 있다.
glmnet(
x, # input matrix
y, # response variable
lambda = NULL, # lambda sequence
alpha = 1, # type of penalty
standardize = TRUE, # x variable standardization
family = c("gaussian", "binomial", "poisson", "multinomial", "cox", "mgaussian"),
...
)
Ridge Regression : glmnet() 함수 + alpha = 0
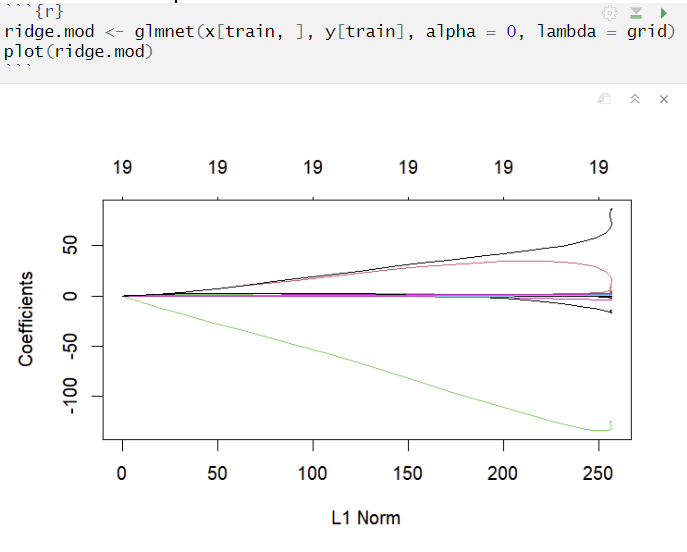
모델 적합
- λ값이 커질수록 regularization 강함 = 회귀계수 추정량 작아짐 = 추정량의 L1 norm 감소
- Rigde에서는 회귀계수 추정량이 매우 낮아지더라도 그 값이 0이 잘 되진 않음
항상 19개의 변수 모두 사용, 변수 선택의 기능이 없음
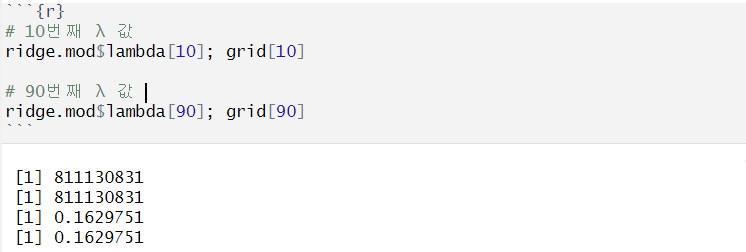
grid에서 각 λ값 확인
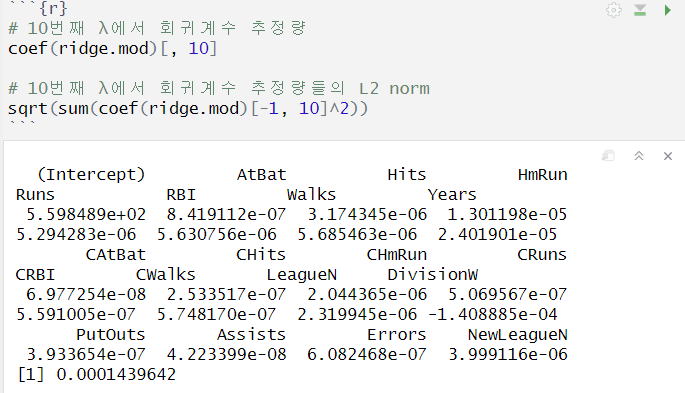
각 λ에서 회귀계수 추정량 확인
- 20개의 X변수 * 100개의 λ값 행렬

- λ_10 > λ_90 = λ_10이 λ_90보다 penalty가 더 강함
= λ_10인 경우 회귀계수 추정량 값이 더 작아짐
= λ_10인 경우 회귀계수 추정량의 L2 norm이 더 작아짐
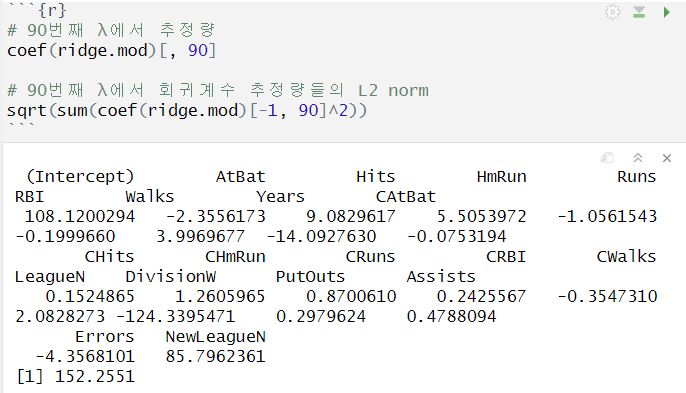
원하는 λ 값에서의 회귀계수 추정량 확인
- predict 함수, s로 λ값 지정, type = "coefficients"
- λ = 0 → regularization을 사용하지 않는 일반적인 LSE 기반 회귀계수 추정량

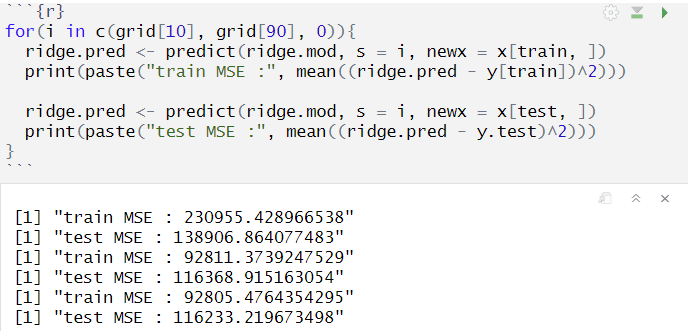
특정 λ값에서 회귀계수 추정량으로 예측 + train/test MSE 계산
- predict 함수, newx = 예측할 데이터
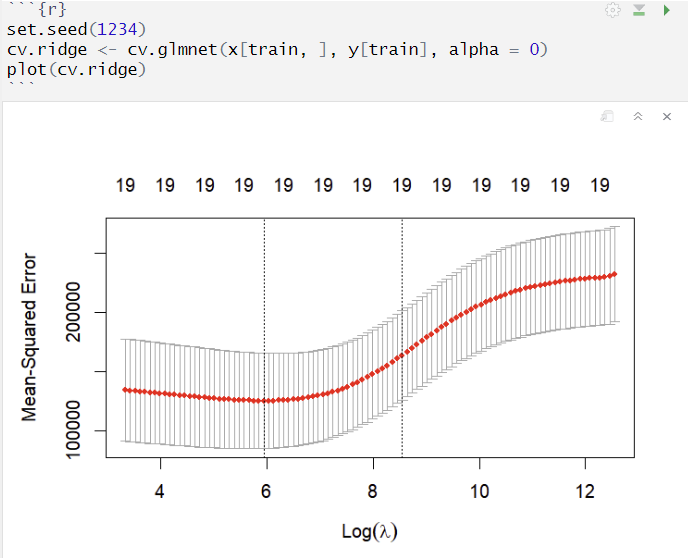
CV로 최적의 λ 정하기
- cv.glmnet() 함수 이용, default는 10-folds CV 수행
- 상단 숫자 : 사용된 X 변수의 개수, Ridge regression은 변수 선택의 기능이 없음
- y축 : 각 lambda에서 cv의 평균 MSE
오류 막대 : 각 lambda에서 평균 MSE의 표준오차 범위
최적의 λ값 확인

최적의 λ값일때 Ridge regression 회귀계수 추정량 확인

최적의 λ값에서 회귀계수 추정량으로 예측, train/test MSE 계산

Lasso Regression : glmnet() 함수 + alpha = 1
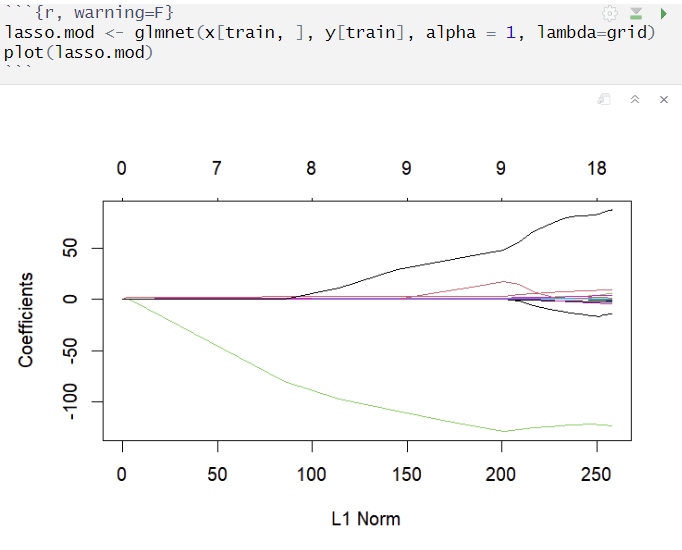
모델 적합
- λ값이 커질수록 regularization 강함 = 회귀계수 추정량 작아짐 = 추정량의 L1 norm 감소
- Lasso에서는 regularization이 강해지면 회귀계수 추정량이 0이 되는 변수가 발생
Ridge와 달리 변수 선택의 기능이 존재, λ값이 커질수록 사용되는 X 개수 감소
CV로 최적의 λ 정하기
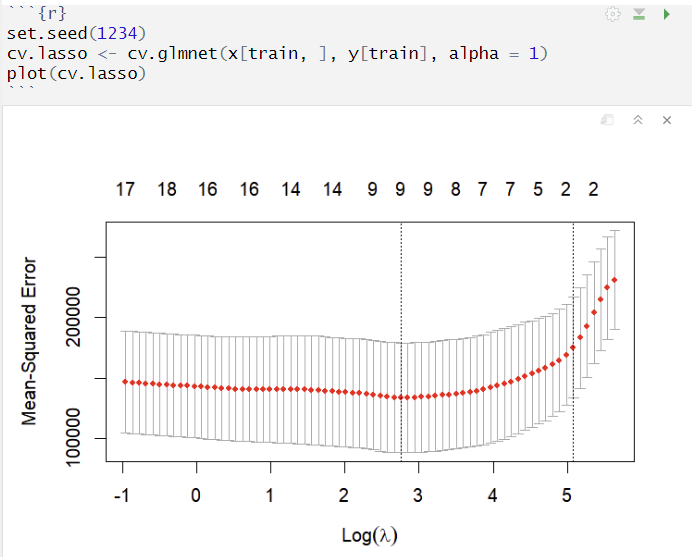
최적의 λ값 확인

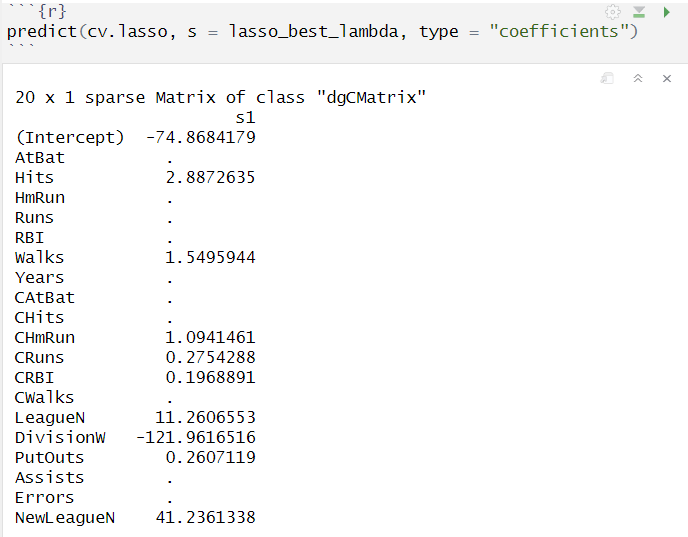
최적의 λ값일때 Lasso regression 회귀계수 추정량 확인
- Ridge와 달리 회귀계수 추정량이 0이 되는 X 변수가 존재
- 기존의 19개의 변수 중 6개 변수의 회귀계수 추정량이 0이 되어 최적 모델에서는 13개의 변수만 사용
최적의 λ값에서 회귀계수 추정량으로 예측, train/test MSE 계산

Ridge와 Lasso 결과 비교
test mse를 비교한 결과 ridge regression 모델이 더 적합한 것으로 판단

최종 모델 = 전체 데이터에 대하여 최적의 ridge λ값에서 적합한 ridge regression 모델
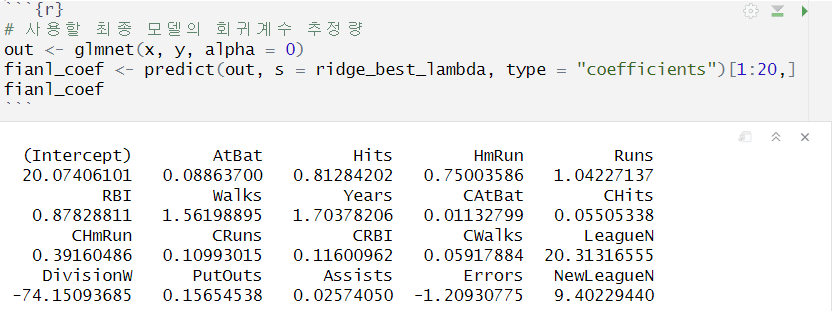
Reference
https://syj9700.tistory.com/29
https://direction-f.tistory.com/75
https://www.rdocumentation.org/packages/glmnet/versions/4.1-8/topics/glmnet
'교내 수업 > R 통계분석' 카테고리의 다른 글
| [R로 하는 통계분석] Piecewise polynomial regression, Splines (0) | 2024.11.25 |
|---|---|
| [R로 하는 통계분석] Classification 모델 적합과 평가 (0) | 2024.11.20 |
| [R로 하는 통계분석] Linear Regression / GLM (0) | 2024.11.03 |
| [R로 하는 통계분석] Bootstrap 신뢰구간 추정 (0) | 2024.11.03 |
| [R로 하는 통계분석] Data Visualization (0) | 2024.11.02 |




