working_helen
[R로 하는 통계분석] Linear Regression / GLM 본문
1. Generalized Linear Model
(1) Logistic Regression
(2) Poisson Regression
(3) Negative Binomial Regression
(4) Zero-inflated Poisson Regression
2. R 코드로 구현하기
1. Generalized Linear Model (GLM)
Linear regression model은 선형성, 정규성, 등분산성, 독립성을 가정
- 반응변수 Y가 정규분포를 따른다
- 설명변수 X와 Y가 선형 관계에 있다

GLM
= Linear regression model의 일반화
= link function을 사용함으로써 더 다양한 종류의 분포를 따르는 Y를 X들 간 선형결합으로 표현할 수 있는 모델
- Y가 정규분포를 포함하는 지수족(exponential family) 분포를 따른다
- 설명변수 X와 E(Y)의 함수가 선형 관계에 있다

- β = (β0, β1, β2 … βp)' : parameters, p개의 파라미터, px1
- X = (x1, x2 ... xn)' : 설명변수 행렬, p차원 데이터 n개, nxp
- Xβ : linear predictor
- g : link function
✅ link function : E(Y)를 설명변수들의 선형결합으로 표현할 수 있도록 변환하는 역할
주어진 데이터의 분포를 바탕으로, Y가 지수족 내 어떤 확률분포를 따를지 가정하고, 각 확률분포에 적합한 link fuction을 사용해 regression을 수행
| Y의 분포 | regression 종류 | link function |
| N(μ, sigma) | Linear Regression | E(Y) = μ f(μ) = μ = Xβ identity function |
| Bern(Θ) | Logistic Regression | E(Y) = P(Y=1) = Θ f(Θ) = logit(Θ) = log(Θ/(1- Θ)) = Xβ logit function |
| Poisson(Λ) | Poisson Regression | E(Y) = Λ f(Λ) = log(Λ) = Xβ log function |
| Negative Binomial(r, p) | Negative Binomial Regression | E(Y) = rp/(1-p) = Λ f(Λ) = log(Λ) = Xβ log function |
| Bern(Θ) + Poisson(Λ) |
Zero-inflated Possion Regression | logit function + log function |
(1) Logistic Regression
Y ~ Bern(Θ)
link function = logit function

- E(Y) = P(Y=1) = Θ
f(Θ) = logit(Θ) = log(Θ/(1- Θ)) = Xβ
- β = logt(평균)의 변화량 = log(오즈비)의 변화량
- βj > 0 : xj가 증가하면 log(오즈비)가 증가한다 = 오즈비가 증가한다 = P(Y=1)이 증가한다 = Y와 xj는 양의 관계에 있다.
(2) Poisson Regression
Y ~ Poisson(Λ), E(Y) = Λ
link function = log function
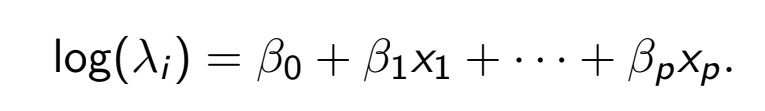
- E(Y) = Λ
f(Λ) = log(Λ) = Xβ
- β = log(Y 평균)의 변화량
- βj > 0 : xj가 증가하면 log(평균)이 증가한다 = 평균이 증가한다 = Y와 xj는 양의 관계에 있다.
(3) Negative Binomial Regression
Y ~ NB(r, p), rp/(1-p) = Λ
link function = log function
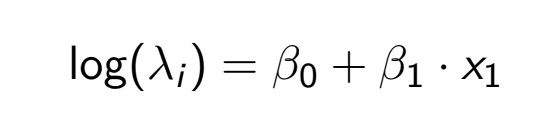
- E(Y) = rp/(1-p) = Λ
f(Λ) = log(Λ) = Xβ
- β = log(Y 평균)의 변화량
- βj > 0 : xj가 증가하면 log(평균)이 증가한다 = 평균이 증가한다 = Y와 xj는 양의 관계에 있다.
✏️ Poisson Regression과 Negative Binomial Regression의 차이점
- Poisson 분포에서는 1개의 파라미터 Λ만 사용 → E(Y) = Λ이고 Var(Y) = Λ임을 가정
- 하지만 실제 데이터에서는 평균에 비해 분산이 큰 경우가 많고, 이때 Poisson 분포를 가정하게 되면 데이터의 분산을 과소평가하게 되는 문제가 발생 = overdispersion 문제
- 이와 달리 NB 분포는 2개의 파라미터를 사용함으로써 평균과 분산을 다른 값으로 둘 수 있기 때문에 동일한 link function을 사용하지만 데이터의 분산이 평균에 따라 증가할 수 있도록 모델링할 수 있음
∴ Poisson 분포의 overdispersion 문제가 의심되는 경우 NB 분포를 사용하여 해소할 수 있다!
(4) Zero-inflated Poisson Regression
Y ~ Bern (Θ) + Y ~ Poisson(Λ)
link function = logit function + log function
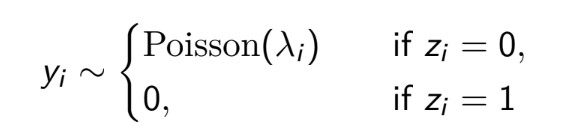
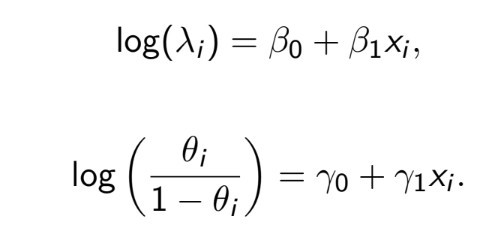
- Y의 분포가 0을 제외한 구간에서는 Poisson 분포를 따르지만, 0에 해당하는 빈도 수가 지나치게 많은 경우에 사용
- 추가적인 확률변수 z : z=1인 데이터에선 모두 Y=0
- z가 Θ의 확률로 0가 되는 경우, 모든 Y값이 0이 되고
z가 1-Θ의 확률로 1이 되는 경우, Y값은 Poisson 분포를 따른다고 가정
- P(z=1) = Θ
f(Θ) = logit(Θ) = log(Θ/(1- Θ)) = Xr
- rj > 0 : xj가 증가하면 P(z=1)이 증가한다 = 0에서 Y의 빈도가 증가한다
- E(Y) = Λ when z≠1
f(Λ) = log(Λ) = Xβ
- βj > 0 : xj가 증가하면 Y 평균이 증가한다 = Y와 xj는 양의 관계에 있다.
2. R 코드로 구현하기
simple linear regression
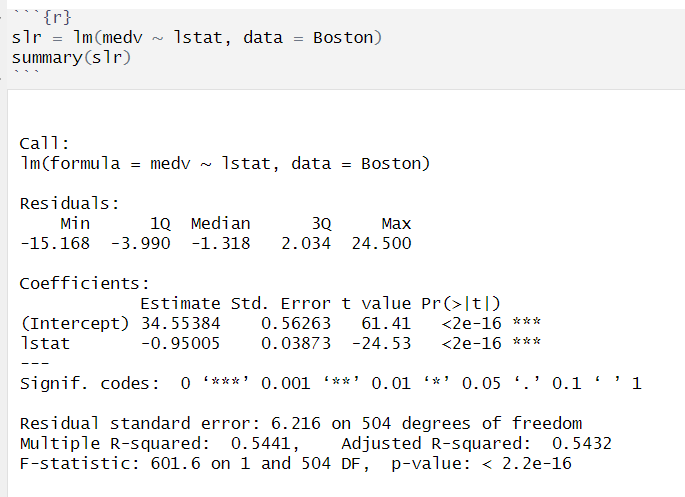
simple linear regression with interaction term
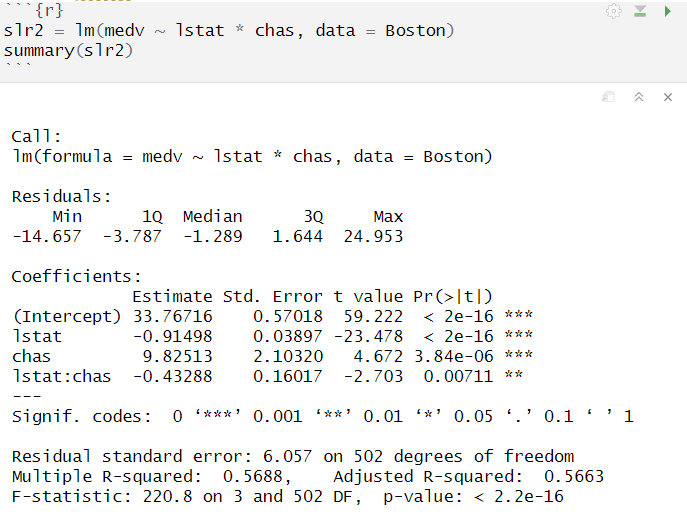
multiple linear regression
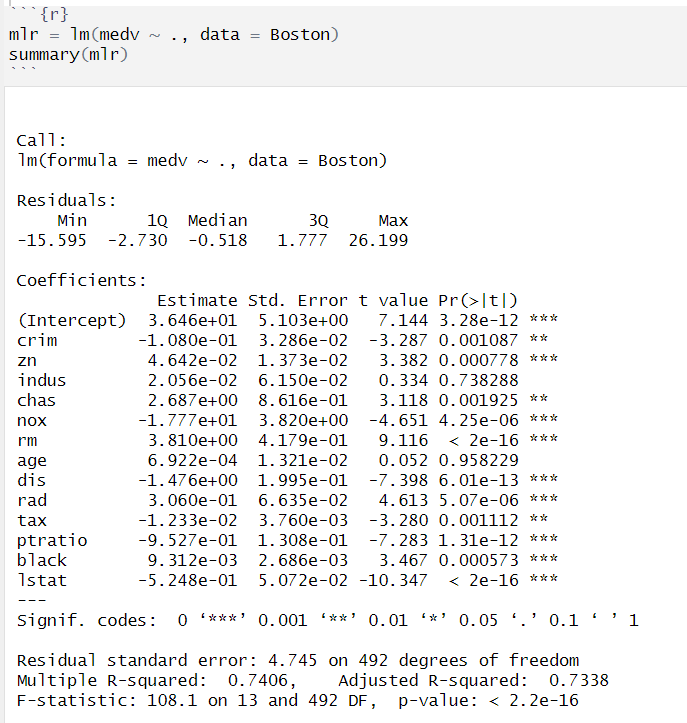
polynomial regression
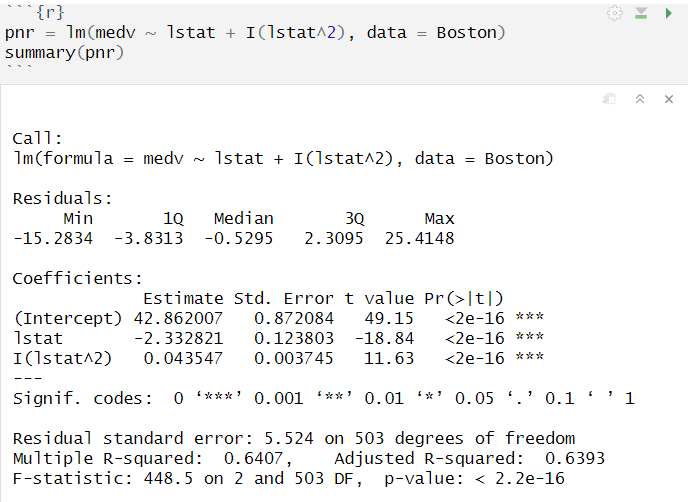
logistic regression
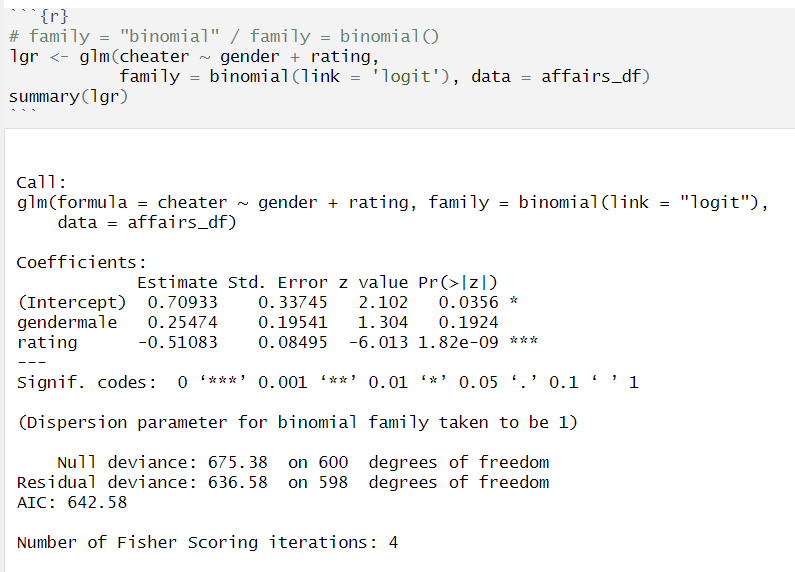

poisson regression
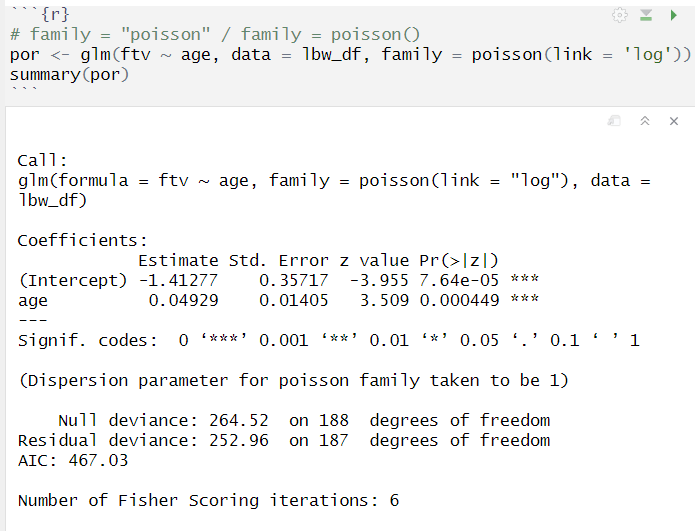

NB regression
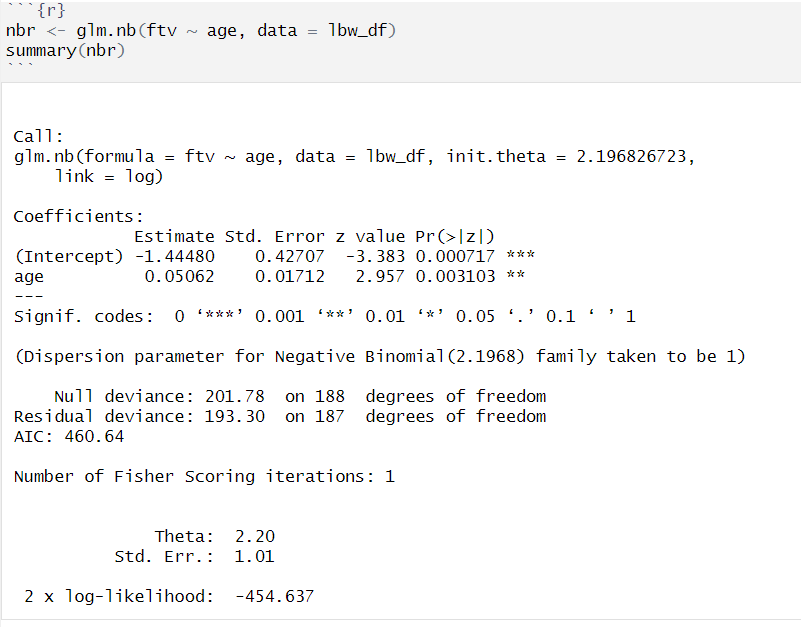

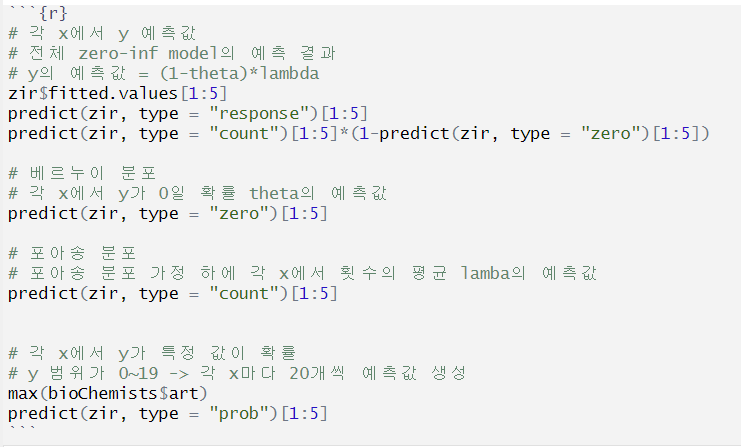
zero-inflated poisson regression
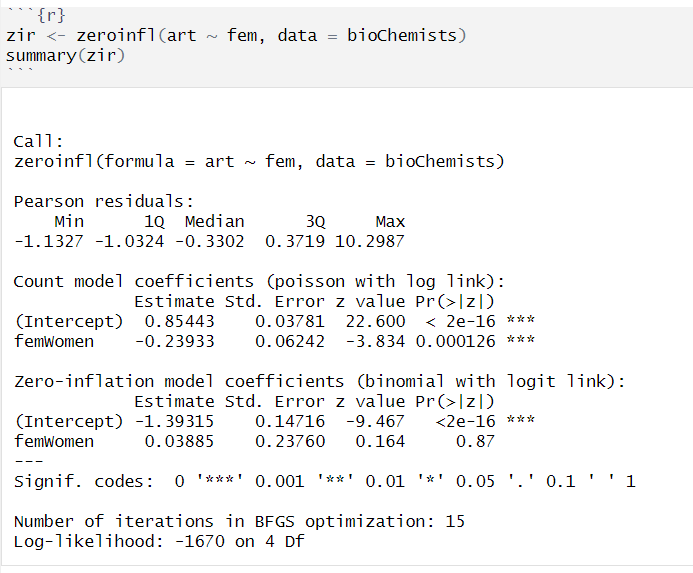
Reference
https://kjhov195.github.io/2019-10-30-generalized_linear_model/
https://be-favorite.tistory.com/52
https://zephyrus1111.tistory.com/26
'교내 수업 > R 통계분석' 카테고리의 다른 글
| [R로 하는 통계분석] Piecewise polynomial regression, Splines (0) | 2024.11.25 |
|---|---|
| [R로 하는 통계분석] Classification 모델 적합과 평가 (0) | 2024.11.20 |
| [R로 하는 통계분석] Linear Regression feature selection (0) | 2024.11.09 |
| [R로 하는 통계분석] Bootstrap 신뢰구간 추정 (0) | 2024.11.03 |
| [R로 하는 통계분석] Data Visualization (0) | 2024.11.02 |



