working_helen
[R로 하는 통계분석] Piecewise polynomial regression, Splines 본문
1. Piecewise polynomial regression
2. Spline
3. Spline R 코드로 구현하기
1. Piecewise polynomial regression
(1) piecewise polynomial regression
- 설명변수 X를 여러 개의 구간을 분할하고, 각 구간마다 별도의 다항회귀모형을 적합하는 방법
- 구간마다 각각 LSE를 적용해 회귀계수 β를 추정
- knots : 회귀모형이 바뀌는 X의 지점, K개의 knots가 있으면 K+1개의 구간이 생성

(2) basis function
- piecewise polynomial regression은 basis function approach의 일종
- 이미 알고있는 basis function(기저 함수) K개의 선형결합으로 y를 표현
- 모델의 자유도 = basis function의 개수

2. Spline

- 좌상단 : 3차 Piecewise polynomial regression
- 우상단 : 3차 Regression Spline
- 좌하단 : 3차 Cubic Spline
- 우하단 : 3차 Nutural Spline
(위키백과) 스플라인 곡선 : 주어진 복수의 제어점을 통과하는 부드러운 곡선으로, 인접한 두 점 사이에의 구간마다 별도의 다항식을 이용해 곡선을 정의. 자연스러운 곡선을 그리는 데 이용된다. n차 스플라인 곡선은 n차 다항식을 이용한 것이지만, 일반적으로 스플라인 곡선은 3차 곡선을 이용.
- piecewise polynomial regression은 구간별로 적합된 다항함수가 knots에서 불연속이 될 수 있다는 문제점 존재
- Spline은 기존의 piecewise polynomial regression에 제약조건을 추가하여 연속의 부드러운 다항식 곡선을 적합하는 방법
- Regression Spline : knots에서 연속 조건
- Cubic Spline : knots에서 연속이고 미분가능, 1, 2차 도함수가 연속 조건
- Natural Spline : Cubic Spline + boundary에서 linear 조건
- Smoothing Spline : Natural Spline with all data + regularization term
Regression Spline
: piecewise polynomial regression + 모든 knots에서 연속 조건
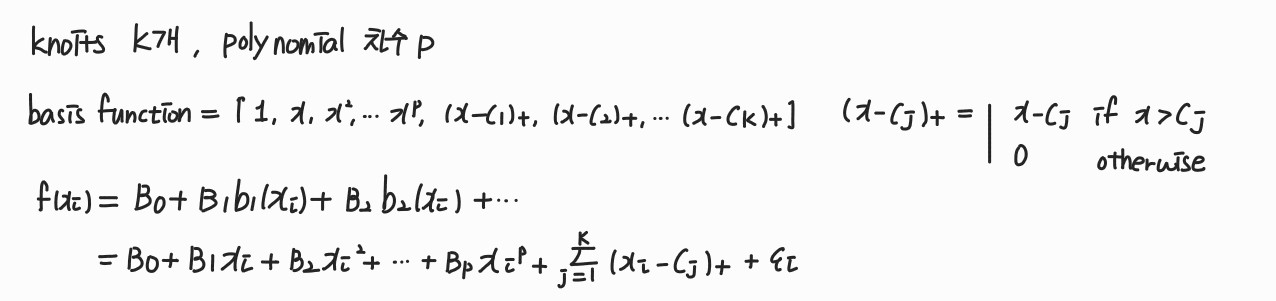
Cubic Spline
: piecewise polynomial regression + 모든 knots에서 연속이고 미분가능

- 모든 구간에서 intercept, 1차항과 2차항 회귀계수를 공유, 3차항 회귀계수만 구간별로
- K개의 knots → 추정해야하는 하는 β = 3 + (K +1) = K + 4개
Natural Spline
: cubic splie + boundary에서 linear 조건

- cubic spline은 범위의 양끝에서 값이 크게 변동하는 문제가 존재
- 범위의 양끝점에 data에 존재하는 점을 지나가도록 제한조건 추가
- 자유도 15 natural cubid spline과 15차항 polynomial regression 비교

Smoothing Spline
: natural spline + overfitting 방지를 위해 loss function에 regularization term 추가

- g(x) : natural spline 함수
- n : data (x, y) 개수
- λ : regularization parameter
- smoothing spline = 위 식을 최소화하는 g(x), β
- 주어진 data 속 모든 x를 knots로 사용하는 natural spline을 진행
+ loss function에 regularization term 추가함으로써 overfitting 방지
- λ = 0 : n개의 knots를 모두 지나는 natural spline, overfitting
- λ ↑ : spline이 점점 더 smooth
3. Spline R 코드로 구현하기
"ISLR2" 패키지 Wage 데이터셋 사용

basis function
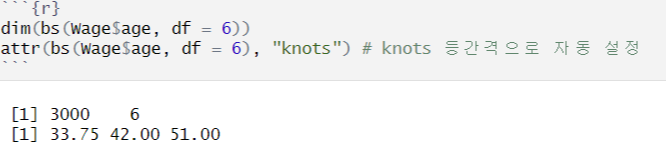
- `bs(x)` : 기저함수 설정, default는 x의 3차항까지
- knots를 지정하는 경우 : knots = K개 → df = (K + 4) -1 = K + 3

- df를 지정하는 경우 : df = df → knots 개수 = (df + 1) - 4 = df - 3
cubic spline fitting
- `lm` 함수를 이용
- knots K개 → K+4개의 회귀계수 적합
모델 자유도 = K+4, 잔차 자유도 = n - (K+4)
- knots 개수 K = 3 → 회귀계수 3+4 = 7개
모델 자유도 = 7, 잔차 자유도 = 3000-7 = 2993

새로운 데이터 예측
- `pred$fit` : 각 x에서 모델의 예측 결과
- `pred$se.fit` : 각 x에서 standard error
- `pred$df` : 잔차 자유도 = n - (K+4)

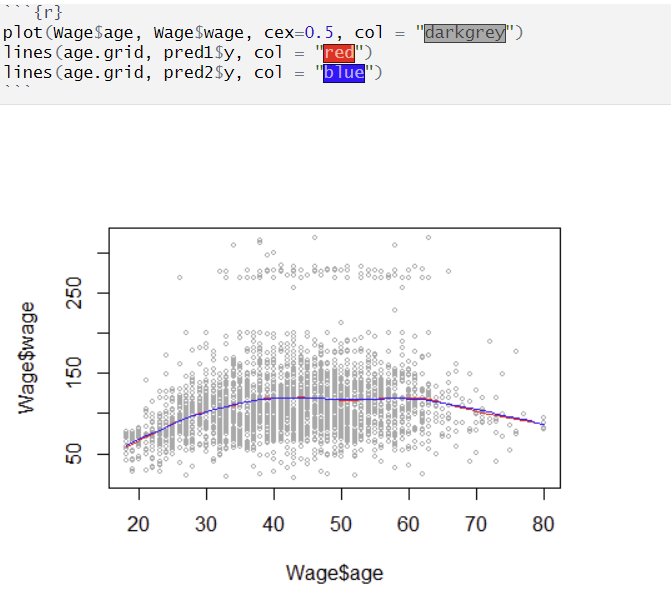
예측 결과 시각화

smooth spline fitting
- `smooth.spline` 함수 이용
- 자유도 지정하는 경우 → 해당 자유도에 해당되는 λ 사용

- `cv = T` → CV를 통해 최적의 λ 결정

새로운 데이터 예측
- `pred$y` : 각 x에서 모델 예측 결과

예측 결과 시각화
Reference
https://en.wikipedia.org/wiki/Segmented_regression
https://ko.wikipedia.org/wiki/%EC%8A%A4%ED%94%8C%EB%9D%BC%EC%9D%B8_%EA%B3%A1%EC%84%A0
https://direction-f.tistory.com/85
https://direction-f.tistory.com/87
https://blog.naver.com/je1206/220804048936
본 포스팅은 James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning with Applications in R. Springer. 책을 참고하여 작성했습니다.
'교내 수업 > R 통계분석' 카테고리의 다른 글
| [R로 하는 통계분석] GAM(Generalized Additive Models) (0) | 2024.11.29 |
|---|---|
| [R로 하는 통계분석] Classification 모델 적합과 평가 (0) | 2024.11.20 |
| [R로 하는 통계분석] Linear Regression feature selection (0) | 2024.11.09 |
| [R로 하는 통계분석] Linear Regression / GLM (0) | 2024.11.03 |
| [R로 하는 통계분석] Bootstrap 신뢰구간 추정 (0) | 2024.11.03 |




