working_helen
[Linear Algebra] SVD를 이용한 image compression 본문
인공지능 CV 분야의 SVD를 이용한 image compression 과정에 대해 학습한다.
1. SVD
2. Low-Rank approximation
3. Image Compression (이미지 압축)
4. 실습 코드
1. SVD (Singular Value Decomposition, 특이값분해)
: 모든 실수 행렬에 사용할 수 있는 행렬 분해 (matrix factorization)
1) A = UΣV'


| U | mxm orthogonal matrix | AA'의 고유벡터를 각 열로 하는 행렬 |
| V | nxn orthogoanl matrix | A'A의 고유벡터를 각 열로 하는 행렬 |
| Σ | mxn diagonal matirx | A의 고유값을 대각성분으로 하는 행렬 np.sqrt(A'A 혹은 A'A의 고유값) 값을 대각성분으로 하는 행렬 |
2) U, V, Σ 계산 과정

→ U : AA' 행렬의 고유값 분해
→ V : A'A 행렬의 고유값 분해
→ D = Σ 'Σ = Σ Σ ' : AA' 또는 A'A의 고유값을 대각성분으로 하는 대각행렬
Σ = np.sqrt(D의 각 성분)
→ U의 각 열 - V의 각열 부호(방향) 맞추기
3) SVD 종류
① reduced SVD
- Σ에서 대각원소가 0인 부분을 제외하고, reduced된 행렬을 인수분해하는 방법
- r = min(m, n) = rank(Σ) (Σ가 고유값 대각행렬로 변환되는 것이므로)
② Compact SVD
- 일부 고유값이 0일때
- Σ에서 대각 원소가 0인 부분 + 값이 0인 고유값을 모두 제거하여 인수분해하는 방법
③ Runcated SVD
- Σ에서 0은 아니지만 정보량이 작은 특이값을 0으로 변환하여 Compact SVD를 진행하는 방법
- 정보량이 적어 유의마하지 않은 고유값을 제거함으로써 차원이 감소된 A의 근사행렬을 인수분해
- k = rank(새로운 Σ_t) ≤ rank(Σ)
2. Low-Rank approximation

- 주어진 행렬 A를 더 낮은 rank의 행렬 A_k로 근사하는 문제
- 주어진 행렬 A를 k개의 특이값, k개의 특이벡터만 사용하여 표현
- 행렬로 표현되는 고차원 데이터를 낮은 차원에서 처리하기 위한 과정이다.
- 데이터의 차원 축소 측면에서 PCA와 유사한 목적을 가진다.
3. Image Compression (이미지 압축)
- image = pixcel matrix = 각 픽셀의 색상(RGB) 강도를 원소로하는 직사각형 행렬
- n = 수직 픽셀 수 / m = 수평 픽셀 수
- color image = n × m ×3 크기의 3차원 배열
- Low-Rank approximation의 활용 분야
- 3가지 색상의 image matrix에 SVD를 적용
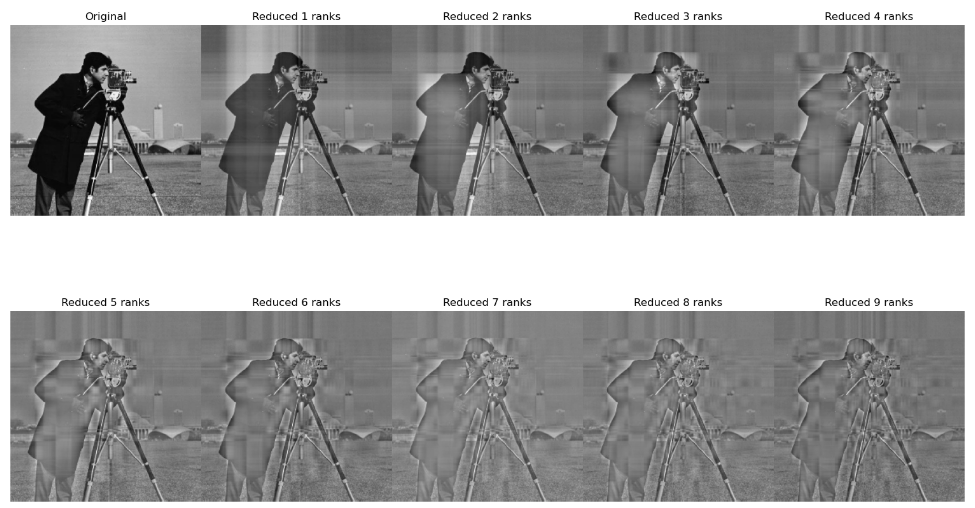
- 가장 큰 특이값에서 작은 특이값으로 하나씩 0으로 설정하고,
- 원본의 feature가 남아있는 수준까지 rank의 수를 줄여나감으로써
==> 원본 이미지의 중요한 feature하고, 이미지 데이터의 크기는 줄인다.
- Image Compression의 기능
- 이미지 데이터 저장 공간을 줄일 수 있다.
- 고차원 이미지 데이터에서 필요한 feature만 추출할 수 있다.
- 고차원 데이터에 포함되어 있는 노이지를 제외시킬 수 있다.
- 압축된 이미지는 압축되지 않은 이미지보다 더 빠르게 저장 및 이동될 수 있다.
4. 실습 코드 - Jupyter notebook
1) SVD 함수 생성
- input = A : (n,m) numpy array
- output = U : (n,n) numpy array
Sig : (min(n,m), 1) numpy array
V : (m,m) numpy array
① SVD 함수 직접 정의
def SVD(A :np.array): # assume 2D array
A = A.astype(np.float32)
n, m = A.shape
U, V, Sig = None, None, None
# U 구하기 : A@(A.T) 고유값 분해
U_eig_val, U_eig_vec = np.linalg.eig(A@(A.T))
U_idx = U_eig_val.argsort()[::-1]
U = U_eig_vec[:, U_idx]
# V 구하기 : (A.T)@A 고유값 분해
V_eig_val, V_eig_vec = np.linalg.eig((A.T)@A)
V_idx = V_eig_val.argsort()[::-1]
V = V_eig_vec[:,V_idx]
# Sigma 구하기 : 0 추가해서 차원 맞추기
if n>=m:
Sig = np.sqrt(V_eig_val)
Sig = Sig[V_idx]
Sig = np.diag(Sig)
zeros = np.zeros((n - m, m))
Sig = np.vstack((Sig, zeros))
if n<m:
Sig = np.sqrt(U_eig_val)
Sig = Sig[U_idx]
Sig = np.diag(Sig)
zeros = np.zeros((n, m-n))
Sig = np.hstack((Sig, zeros))
# SVD 이후에 나타난 부호 불일치 수정
for i in range(min(n, m)):
u_i = (A@V@Sig.T)[:, i]
if np.dot(u_i, U[:,i]) < 0:
for j in range(len(u_i)):
if(U[j,i] !=0):
U[j,i] = -U[j,i]
return U, Sig, V
② np.linalg.svd() 이용
def SVD_tool(A :np.array):
n,m = A.shape
print(n,m)
U, s, Vt = np.linalg.svd(A)
Sigma = np.diag(s)
print(Sigma)
if n>m:
zeros = np.zeros((n - m, m))
Sigma = np.vstack((Sigma, zeros))
if n<m:
zeros = np.zeros((n, m-n))
Sigma = np.hstack((Sigma, zeros))
return U, Sigma, Vt.T
실행 결과 비교

2) image copression
import cv2
import copy
original_img = cv2.imread("이미지 경로", cv2.IMREAD_UNCHANGED)
original_img = original_img.astype(np.float32)
# Sigma rank 감소시키는 함수
def compress(Sigma, rank=0):
Sigma[:rank]=0
return Sigma
img_list = []
img_list.append(original_img)
# 원본 이미지로 SVD 실행
U, Sig, Vt = None, None, None
U, Sig, V = SVD(original_img)
# SVD로 구한 Sigma에 rank 1개씩 감소시켜보기
for rank in range(1,10):
reduced_Sig = compress(Sig, rank)
reduced_img = U@reduced_Sig@V.T
img_list.append(reduced_img)
Reference
https://www.cloudflare.com/ko-kr/learning/performance/glossary/what-is-image-compression/
https://zerobone.net/blog/cs/svd-image-compression/
https://velog.io/@rkdtjdals97/SVDSingular-Value-Decomposition-%ED%8A%B9%EC%9D%B4%EA%B0%92-%EB%B6%84
https://communities.sas.com/t5/SAS-Tech-Tip/SAS-%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D-SVD%EB%A5%BC-%EC%9D%B4%EC%9A%A9%ED%95%9C-%EC%9D%B4%EB%AF%B8%EC%A7%80-%EC%95%95%EC%B6%95-Image-compression/ta-p/662912
'교내 수업 > 인공지능' 카테고리의 다른 글
| [NLP] Language Model / n-gram, NNLM, RNNLM (1) | 2024.01.30 |
|---|---|
| [NLP] Word2Vec / Skip-gram, CBOW (0) | 2024.01.29 |
| [CNN] CNN 모델의 발전 (1) | 2024.01.21 |
| [CNN] Convolution Layer / Pooling layer (1) | 2024.01.21 |
| [CNN] Fully-Connected Layer (0) | 2024.01.19 |




