working_helen
[Audio feature 군집화] Spotify Song Clustering with k-means 본문
[Audio feature 군집화] Spotify Song Clustering with k-means
HaeWon_Seo 2023. 9. 16. 00:11앞서 학습한 k-means 군집화 알고리즘을 적용하여 Spotify 노래 데이터 clustering하는 과정에 대해 정리해본다. 본 프로젝트에서는 audio feature를 이용해 노래의 mood cluster를 구하는 과정을 진행했다.
참고한 이전 분석 자료
International Journal of Music Science, Technology and Art
IJMSTA - Vol. 5 - Issue 1 - Janury 2023 ISSN 2612-2146 Pages: 13 Spotify Song Analysis by Statistical Machine Learning Authors: Federica Biazzo, Matteo Farné Categories: Journal Abstract - This paper aims to study the use of Artificial Intelligence in the
www.ijmsta.com
Music Recommendation System using Spotify Dataset
Building Mood-Based Spotify Playlists using K-Means Clustering
1. 군집화 알고리즘
1) 군집화 알고리즘의 종류
2) k-means를 사용한 이유
2. Scaling
1) Scaler 종류
2) MinMaxScaler를 사용한 이유
3. 변수 PCA
4. k-means clustering
5. clustering 결과
1) 시각화
2) 군집별 특성 확인
1. 군집화 알고리즘
: 비슷한 특성을 가진 데이터끼리 집단을 나누어 레이블링하는 비지도 학습 알고리즘
1) 군집화 알고리즘의 종류
k-means
| 장점 | 단점 |
| - 알고리즘이 쉽고 간결하여 가장 일반적으로 사용한다. - 데이터와 그룹 간 거리 계산에만 의존하기 때문에 계산량이 적고, O(n)의 계산복잡도를 가진다. - 클러스터 내 데이터가 원형으로 흩어져 있는 경우에 효과적 |
- 직접 최적의 군집 수 k를 정해야한다. - 초기 중심점 위치에 따라 클러스터링 결과가 달라질 수 있다. - feature 개수가 매우 많을수록 군집화 정확도가 떨어진다.(PCA 차원 축소를 적용한 후 진행하는 방안) - 평균값을 클러스터 중심점으로 사용한다는 특성으로 인해 군집화가 잘 적용되지 않는 분포가 존재한다. |
GMM(Gaussian Mixture Model)

- 정규분포 기반 군집화 방식
- 주어진 데이터 분포를 k개의 가우시안 분포가 혼합된 것으로 가정하는 방법
- 혼합 가우시안 분포에서 k개의 가우시안 분포를 추출 → 각 데이터가 어느 가우시안 분포에 속하는 추정
- 즉 k개의 가우시안 분포 = k개의 군집
- 각 클러스터의 가우스 파라미터를 찾기위해 Expectation-Maximization(EM) 최적화 알고리즘을 사용
| 장점 | 단점 |
| - 기하학적인 분포의 군집, 서로 겹치는 군집에 대해서도 군집화할 수 있다. - 데이터가 두 개의 클러스터에 겹쳐있는 경우 각 클러스터에 속할 확률을 제시해줌으로써 mixed membership을 지원한다. - 원형 분포만 표현하는 k-means에 비해 더 다양한 분포를 표현할 수 있다. GMM은 표준편차 파라미터 덕분에 원뿐만 아니라 타원 모양의 분포를 표현할 수 있다. 따라서 GMM은 타원형으로 길게 늘어진 데이터 군집화에 효과적이다. |
- k-means와 마찬가지로 군집 개수를 의미하는 가우시안 분포의 개수 k를 직접 정해야한다. - 각 가우시안 분포마다 충분한 데이터들이 있어야, 분포 파라미터 추정이 잘 수행될 수 있다. - k-means에 비해 계산량이 많다. |
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=k값, n_init=10, tol=1e-3, max_iter=1000).fit(df)
#군집 예측 결과 저장
gmm_cluster_labels = gmm.predict(df)
df['gmm_cluster'] = gmm_cluster_labels
#모델 성능 확인
gm.aic(df)
gm.bic(df)
gm.score(df)
- 모델 파라미터
tol : 수렴 임계값, 이 임계값보다 낮으면 EM 반복이 중지, default = 1e-3
max_iter : 수행할 EM 반복 횟수, default = 100
n_init : 수행할 초기화 횟수, default = 1 - 모델 method
aic, bic : AIC, BIC값 반환
score : 데이터셋의 샘플당 평균 log-likelihood 반환

- GMM은 각 클러스터에 속할 확률값을 사용하는 모델이기 때문에 실루엣 계수가 아닌 log-likelihood 기반의 AIC(Akaike Iinformation Criterion)와 BIC(Bayesian Information Criterion)를 사용한다.
- likelihood가 클수록 = log-likelihood가 클수록 = AIC와 BIC값이 작을수록 모델의 성능이 좋다.
- 따라서 GMM은 AIC 또는 BIC가 최소화되는 k를 군집 개수로 삼는다.
DBSCAN(Density Based Spatial Clustering of Applications with Noise)

- 밀도 기반 군집화 방식
- 같은 클러스터에 속하는 데이터는 서로 근접하게 분포할 것이라고 가정하고, 데이터의 밀도가 사전에 지정된 기준 이상인 경우 하나의 클러스터로 구분하는 방식
- DBSCAN 과정
- 클러스터 반경 ε (epsilon) / 반경 내 데이터 최소 개수 minPoints 결정
- step 1. 임의의 데이터 포인트를 선택
- Step 2. 해당 데이터의 종류 판단
데이터를 기준으로 ε 반경 내에 minPoints 개수 이상의 데이터가 있다면 Core point로 할당
데이터를 기준으로 ε 반경 내에 minPoints 개수 이상의 데이터가 없다면 Border point로 할당 - Step 3. 어떤 데이터가 Step 2가 Core point이고, 다른 군집에 할당되어있다면 두개의 군집을 하나로 묶음
- Step 4. 모든 데이터가 클러스터에 할당될 때까지 반복
- Core point도 Border point에도 해당하지 않아서 군집이 되지 않는 point는 Noise point가 된다.
| 장점 | 단점 |
| - k-means나 GMM에 비해 클러스터 분포 형태에 구애받지 않기 때문에 기하학적으로 복잡한 분포의 데이터에도 효과적으 군집화가 가능하다. - 자체 계산 과정을 통해 클러스터 개수가 결정되기 때문에 사전에 클러스터 를 지정할 필요가 없다. - 노이즈에 강하다. |
- 각 클러스터의 밀도가 다양한 경우 군집화가 잘 수행되지 않는다. 밀도가 다양해지면 neighborhood point를 판단하는 거리 임계값 ε 및 minPoints가 클러스터에 따라 크게 달라지기 때문에 일관적인 기준값을 사용하면 군집화가 어려워진다. - 고차원 데이터거나 데이터의 분포를 모르는 경우 적절한 임계값을 설정하기 어렵다. - 데이터가 학습되는 순서에 따라 영향을 받는다. |
2) k-means를 사용한 이유
- audio feature 변수 개수가 많아 시각화 상태에서 데이터 분포를 파악하는게 어려움
→ 고차원 데이터거나 데이터의 분포를 모르는 경우 적절한 임계값을 설정하기 어려운 DBSCAN 제외
- Spofity audio feature 분류와 관련된 이전 분석 자료를 살펴보았을때 대부분 k-means를 사용했기 때문에 가장 일반적인 kmeans를 사용해보기로 결정
- k-means보다 더 범용적인 GMM도 함께 적용해보았으나 결과적으로 GMM과 k-means의 결과가 거의 일치하여 k-means 알고리즘을 최종 모델로 선택함
2. Scaling
- 다차원 데이터에서 feature의 범위나 분포를 동일하게 조정해주는 과정
- 다차원 데이터에서 feature들은 서로 다른 단위를 가지고 있는데, 거리 기반 모델의 경우 단위의 수치적 값이 상대적으로 더 큰 feature가 단순히 단위 차이로 인해 계산 과정에 더 많은 영향을 미칠 수 있다.
- 이러한 문제를 방지하기 위해 모든 feature 단위의 수치적 크기를 동일하게 맞춰주는 scaling을 진행한다.
1) Scaler 종류
StandardScaler
- 각 feature 값에 대하여 해당 feature의 평균을 빼고, 분산으로 나눠주는 표준화 과정을 수행
- 모든 feature가 N(0,1)의 정규분포를 따르게 변환한다.
- 데이터의 정규성을 가정하는 알고리즘을 구현하는 경우 잘 사용된다.
- 이상치의 영향을 크게 받으며, 데이터의 기존 분포 형태를 왜곡할 수 있다는 문제점이 있다.
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
df_scaled = standardScaler.fit_transform(df)
df_scaled = pd.DataFrame(df_scaled, columns=df.columns)
RobustScaler
- StandardScaler과 유사하게 각 feature 값에 대하여 해당 feature의 median을 빼고, IQR로 나눠주는 과정을 수행
- StandardScaler에서 보다 더 넓은 분포 형태로 표준화된다.
- 다른 Scaling 방법에 비해 이상치에 의한 영향을 최소환 기법이다.
- 데이터의 기존 분포 형태를 왜곡할 수 있다는 문제점이 있다.
from sklearn.preprocessing import RobustScaler
robustScaler = RobustScaler()
df_scaled = robustScaler.fit_transform(df)
df_scaled = pd.DataFrame(df_scaled, columns=df.columns)
MinMaxScaler
- 모든 feature에 대하여 최솟값은 0, 최댓값은 1이 되도록 값을 [0, 1] 범위로 변환
- 이상치가 있는 경우 이상치가 끝값이 되어 매우 좁은 범위로 압축될 수 있기 때문에 이상치에 민감하다.
from sklearn.preprocessing import MinMaxScaler
minMaxScaler = MinMaxScaler()
df_scaled = minMaxScaler.fit_transform(df)
df_scaled = pd.DataFrame(df_scaled, columns=df.columns)
MaxAbsScaler
- 모든 feature에 대하여 최소절댓값은 0, 최대절댓값은 1이 되도록 값을 [-1, 1] 범위로 변환
- MinMaxScaler와 유사한 이유로 이상치에 민감하다.
from sklearn.preprocessing import MaxAbsScaler
maxAbsScaler = MaxAbsScaler()
df_scaled = maxAbsScaler.fit_transform(df)
df_scaled = pd.DataFrame(df_scaled, columns=df.columns)
2) MinMaxScaler를 사용한 이유
- 가장 적합한 Scaling 방법은 데이터의 분포나 유형에 따라 달라지기 때문에 분석하고자 하는 데이터의 특성에 맞는 scaling 방법을 적절히 선택해야한다. 일반적으론 StandardScaler를 많이 사용한다.
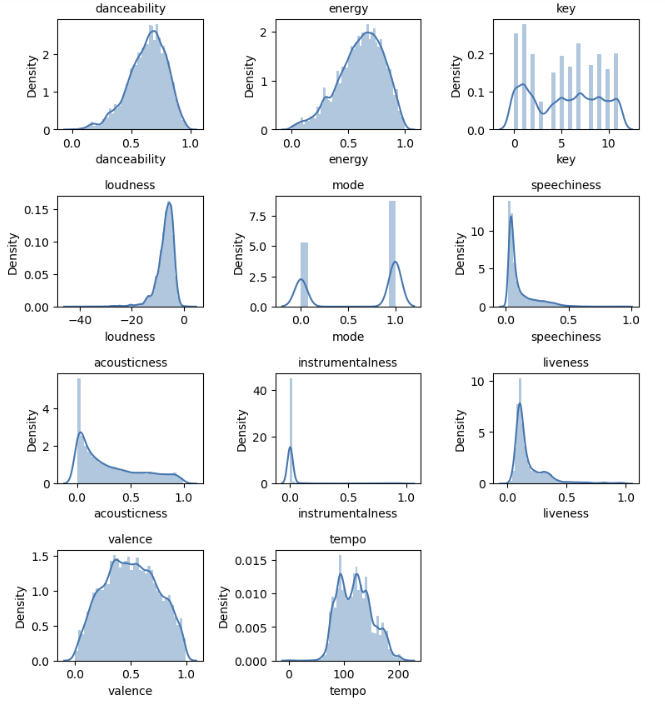
- 본 프로젝트에서 사용한 k-means 알고리즘의 경우 정규분포를 가정할 필요가 없었다.
- 위와 같이 audio feature data의 분포를 확인해보았을때, 값이 한쪽으로 쏠려있지만 중심에서 벗어난 값들이 이상치는 아닌 skewed된 형태의 분포를 보였다. audio feature의 차이로부터 노래를 clustering하는 것이 목표였기 때문에 기존의 노래 간 차이를 드러내는 skewed한 분포를 최대한 변형시키지 않는 것이 적절하다고 판단했다. 이에 따라 StandardScaler와 RobustScaler를 사용하지 않았다.
- 원래 데이터의 범위가 다 양수였기 때문에 MinMaxScaler와 MaxAbsScaler의 결과는 동일하다.
➡️ 따라서 기존 데이터 분포를 잘 보존하고, 양수 범위에서 sacling하는 MinMaxScaler를 사용한다.
3. 변수 PCA
- audio feature 변수가 11개로 많고, 일부 변수는 노래 간 분류에 기여도가 낮을 것이라 예상 (사전 조사)
- k-means의 경우 feature 개수가 매우 많을수록 군집화 정확도가 떨어지는 단점이 있었기 때문에 PCA 수행
- 변수 PCA를 통해 audio feature 변수를 차원 축소한 후, 추출된 PC를 기준으로 k-means를 수행
- PCA 결과 : 분산 설명력 90% 기준 7개, 70% 기준 3개의 PC를 사용
(노래를 가능한 많은 cluster로 나눈는게 목표 + 노래 간 차이를 직접 들어본 후, PC 3개인 경우로 하기로 결정)
4. k-means clustering
- 최적 k값 확인 : Elbow Method 수행 결과 k=6에서 최적
- 실루엣 계수 : SilhouetteVisualizer 이용, 전체 데이터 평균 실루엣 계수 = 0.443279
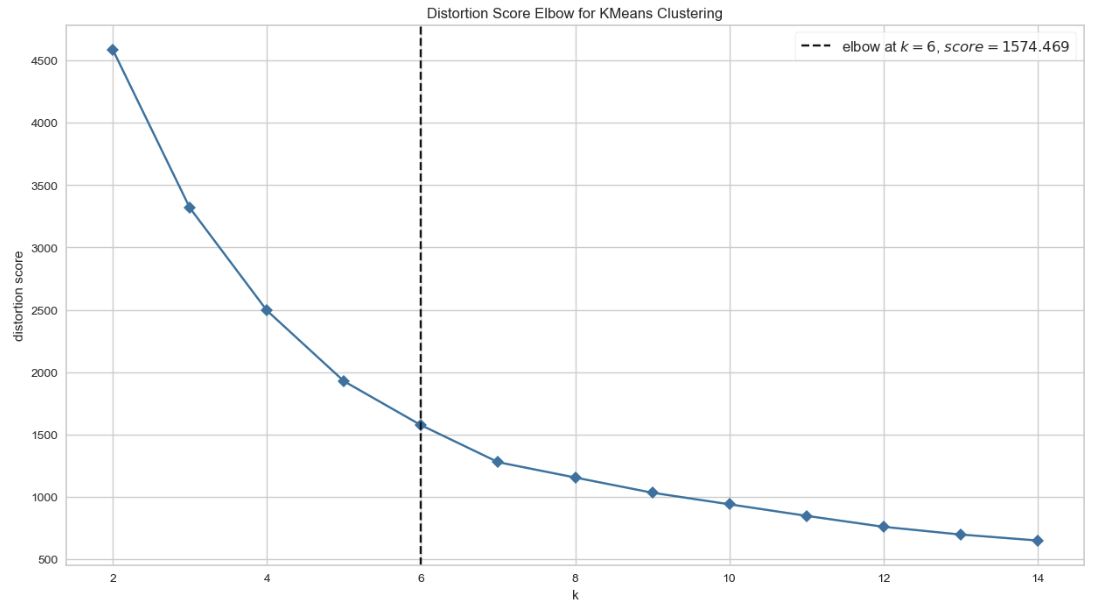
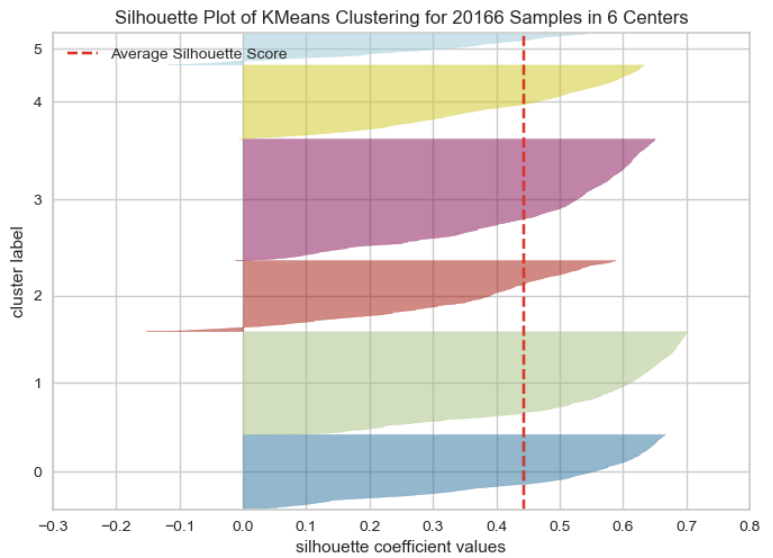
5. clustering 결과
1) 시각화
- feature가 4개 이상인 경우 시각화가 어렵기 때문에 2/3차원으로 차원 축소를 진행해 시각화한다.
t-SNE (t-distributed stochastic neighbor embedding, t-분포 확률적 임베딩)
: 차원 축소 기법의 일종
- 특히 고차원 데이터의 2/3차원 시각화에 유용하게 사용
- 비슷한 데이터는 근접한 2/3차원의 지점으로, 다른 데이터는 멀리 떨어진 지점으로 맵핑한다.
- N개의 데이터에 대해 N^2 시간의 계산이 필요할 정도로 많은 계산이 요구된다.
- PCA : 원본 데이터의 정보를 가장 잘 유지하면서 차원을 줄이는 차원 축소 방법
- t-SNE : 원본 데이터를 가장 잘 표현할 수 있도록 차원을 줄이는 차원 축소 방법
- PCA의 경우 목표가 '데이터의 정보를 가장 잘 보존하는' 것이고, t-SNE의 경우 '원본을 가장 잘 표현할 수 있는' 방식이라는 점에서 차이가 있다. 이로 인해 PCA가 잘 적용되지만 그룹에 따른 차이를 시각화로 확인이 어려운 경우, 동일한 데이터에 대해 t-SNE를 이용해 시각화하면 그룹에 따른 차이를 더 명확하게 확인할 수 있다.
from sklearn.manifold import TSNE
# 2차원 t-SNE 임베딩
tsne_df = TSNE(n_components = 2).fit_transform(df)
tsne_df = pd.DataFrame(tsne_np, columns = ['component 0', 'component 1'])
# 3차원 t-SNE 임베딩
tsne_np = TSNE(n_components = 3).fit_transform(train_df)
tsne_df = pd.DataFrame(tsne_np, columns = ['component 0', 'component 1', 'component 2'])
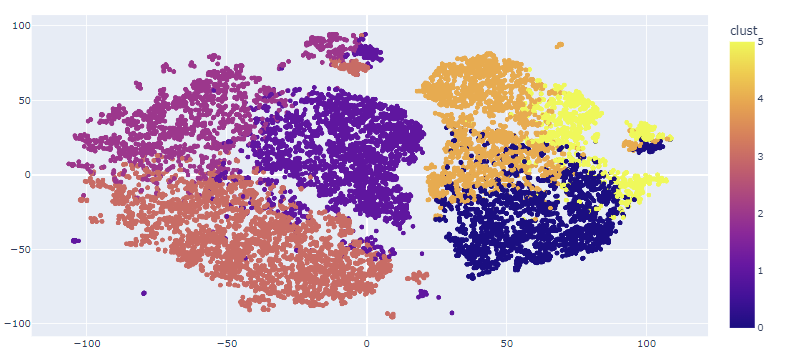
2) 군집별 특성 확인
[audio feature에 대한 변수 설명]
https://developer.spotify.com/documentation/web-api/reference/get-audio-features
Web API Reference | Spotify for Developers
Energy is a measure from 0.0 to 1.0 and represents a perceptual measure of intensity and activity. Typically, energetic tracks feel fast, loud, and noisy. For example, death metal has high energy, while a Bach prelude scores low on the scale. Perceptual fe
developer.spotify.com
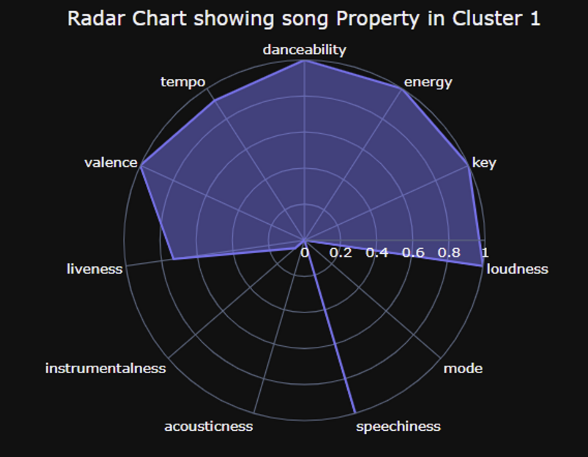
Cluster1
- 박자 타기 좋은 음악
- '악기 소리'는 거의 없고, 탁탁 하는 박자 소리가 중심
- 완전 밝거나 우울하거나 하는 느낌보단 미소 지을 수 있는 정도의 여유로움
- 전주/간주에 비해 가사와 노래가 많음
→ 리듬 타면서 들을 수 있는, 가사 위주 노래
→ 힙합 음악 / 여유로운 카페 음악
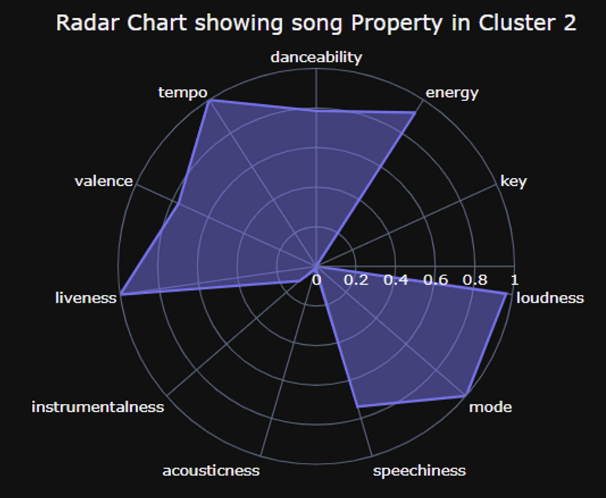
Cluster2
- 속도감은 있는데 노래 자체는 밝지 않음
- 전반적으로 1번보다 더 어두운 느낌으로 들림
- 1과 유사하게 발로 박자 탈 수 있는 수준의 리듬감
- 가사 중심 + 힙합 음악 다수
→ 리드미컬하고 속도감 있는데, 어두운 노래
→ 힙합 음악
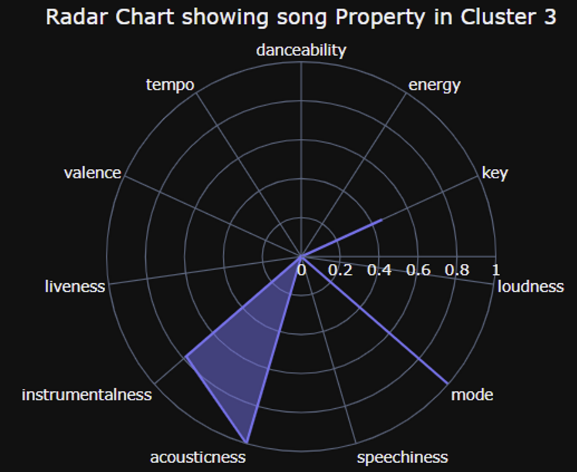
Cluster3
- 박자 소리가 많지 않음, 흘러가는 듯한 배경 음악
- 어둡고, 느리고 잔잔한 느낌의 음악 다수 (발라드)
- 울리는 느낌의 백음악 + 코러스나 화음이 많은 (풍부한 백사운드)
- 1, 2에 비해 가사보다 배경음악이 많은 편
→ 어둡고 잔잔한 노래, 풍부하고 화음이 많은 백음악
→ 어두운 발라드 계열 / 느린 속도의 힙합
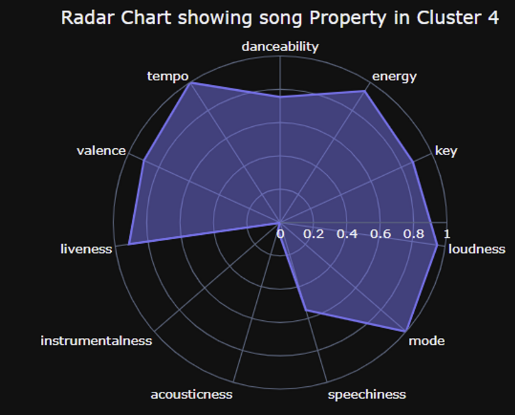
Cluster4
- cluster1과 유사점 = 박자 타기 좋음 음악
- cluster1과 차이점 = 더 어둡고, 늘어지는 느낌(chill)의 곡이 많음, 전주도 더 긴 경향
→ 1과 동일한 결의 음악 중에서 조금 더 어둡고, 느리고, chilling한 음악 계열
→ 리듬 타면서 들을 수 있는, 가사 위주 노래
→ 힙합 음악 / 여유로운 카페 음악
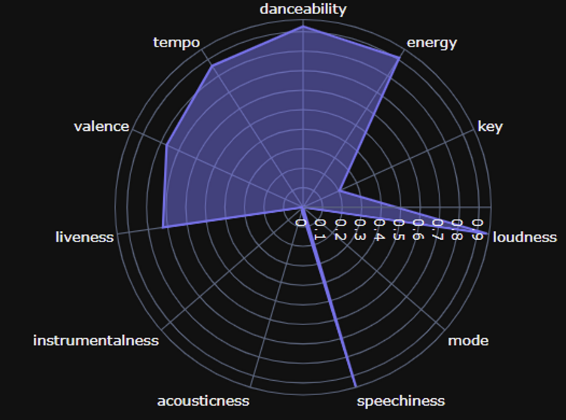
Cluster5
- 막 밝은 느낌의 노래는 아니지만, 완전 우울한 측면도 아님
- 중간에 데시벨 높은 구간이 존재하거나, 그냥 전체적으로 데시델이 큰 노래
- 간주 부분에서 노래만 들려주지 않고, 가사로 채운 형태
→ 어둡고 빠르진 않은데, 높은 데시벨의 가사 구간이 존재하는 노래
→ 어두운 + 웅장함 + 데시벨 높음 + 가사 위주 노래
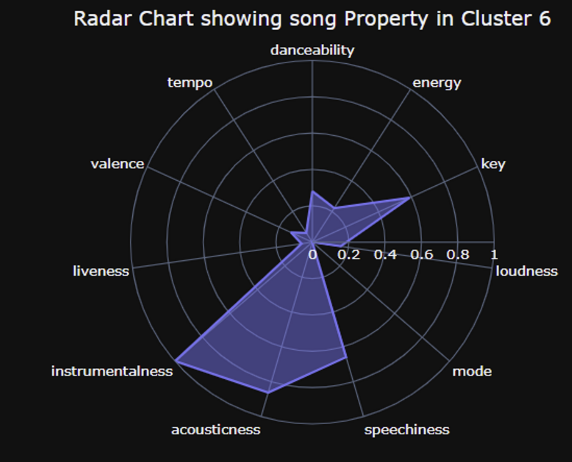
Cluster6
- 느리고 잔잔하고 어두운 계열
- 자신감 저하/고민/생각거리 많은 상태에서 들으면 공감될 것 같은 느낌
-가사 많이 없이 잔잔한 배경 음악 흘러감
Jupyter Notebook
data = pd.read_csv(path + "/데이터 수집/Spotify/노래_전체.csv", index_col=0)
print(data.duplicated().sum())
print(data.isnull().sum())
af = data.iloc[:, 3:]
af
| danceability | energy | key | loudness | mode | speechiness | acousticness | instrumentalness | liveness | valence | tempo | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.529 | 0.469 | 1.0 | -6.967 | 0.0 | 0.0358 | 0.0899 | 0.000015 | 0.8310 | 0.344 | 87.864 |
| 1 | 0.726 | 0.431 | 8.0 | -8.765 | 0.0 | 0.1350 | 0.7310 | 0.000000 | 0.6960 | 0.348 | 144.026 |
| 2 | 0.577 | 0.729 | 7.0 | -7.113 | 1.0 | 0.2210 | 0.3940 | 0.000156 | 0.1440 | 0.692 | 180.065 |
| 3 | 0.629 | 0.585 | 9.0 | -7.969 | 1.0 | 0.0572 | 0.4300 | 0.000000 | 0.3570 | 0.296 | 81.973 |
| 4 | 0.596 | 0.707 | 1.0 | -6.825 | 1.0 | 0.0490 | 0.1110 | 0.000000 | 0.0926 | 0.262 | 133.858 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 7336 | 0.657 | 0.569 | 2.0 | -6.287 | 1.0 | 0.0542 | 0.2010 | 0.000013 | 0.1260 | 0.399 | 102.055 |
| 7337 | 0.524 | 0.141 | 9.0 | -19.818 | 1.0 | 0.0319 | 0.9190 | 0.944000 | 0.0770 | 0.356 | 78.698 |
| 7338 | 0.589 | 0.412 | 11.0 | -6.226 | 0.0 | 0.0363 | 0.7200 | 0.000000 | 0.1530 | 0.703 | 74.954 |
| 7339 | 0.551 | 0.550 | 10.0 | -5.339 | 1.0 | 0.0286 | 0.7770 | 0.000000 | 0.2020 | 0.342 | 101.190 |
| 7340 | 0.621 | 0.108 | 10.0 | -15.399 | 1.0 | 0.0493 | 0.9680 | 0.000017 | 0.1370 | 0.204 | 129.285 |
20166 rows × 11 columns
MinMax Scaling
from sklearn.preprocessing import MinMaxScaler, StandardScaler
min_max_scaler = MinMaxScaler()
stand_scaler = StandardScaler()
af_scaled = min_max_scaler.fit_transform(af)
af_scaled = pd.DataFrame(af_scaled, columns=af.columns)
af_scaled.describe()
| danceability | energy | key | loudness | mode | speechiness | acousticness | instrumentalness | liveness | valence | tempo | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 | 20166.000000 |
| mean | 0.646087 | 0.610610 | 0.481044 | 0.781377 | 0.621343 | 0.113345 | 0.310262 | 0.041857 | 0.186426 | 0.505750 | 0.561310 |
| std | 0.163310 | 0.198527 | 0.329830 | 0.075191 | 0.485065 | 0.119265 | 0.289792 | 0.167569 | 0.151054 | 0.238896 | 0.140422 |
| min | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 0.545270 | 0.484990 | 0.181818 | 0.752751 | 0.000000 | 0.039334 | 0.057831 | 0.000000 | 0.099798 | 0.325253 | 0.444389 |
| 50% | 0.665310 | 0.631993 | 0.454545 | 0.796163 | 1.000000 | 0.059521 | 0.213855 | 0.000000 | 0.126135 | 0.498990 | 0.555657 |
| 75% | 0.765005 | 0.759995 | 0.727273 | 0.828903 | 1.000000 | 0.138398 | 0.519076 | 0.000131 | 0.224016 | 0.689899 | 0.657110 |
| max | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
audio feature PCA¶
1. PC 개수 결정
pca = PCA()
pca.fit(af_scaled).transform(af_scaled)
exp_var_ratio=pca.explained_variance_ratio_
exp_var_ratio
array([0.37975895, 0.18451986, 0.16402536, 0.08583208, 0.0453769 ,
0.03903699, 0.03046058, 0.02814859, 0.02227753, 0.01747429,
0.00308887])# 각 PC의 설명 비율을 누적합한 array 생성
exp_var_cumul = np.cumsum(pca.explained_variance_ratio_)
# PC의 설명 비율 누적 합 그래프 생성
px.area(
x=range(1, exp_var_cumul.shape[0] + 1),
y=exp_var_cumul,
labels={"x": "# Components", "y": "Explained Variance"},
width=700, height=400
)
3개로 PCA 수행
pca = PCA(n_components=3)
pca.fit_transform(af_scaled)
array([[ 0.53032587, 0.14087362, -0.48366067],
[ 0.56993984, 0.49279403, 0.22072918],
[-0.32623537, -0.17575433, 0.20922209],
...,
[ 0.62489746, 0.40407692, 0.49916526],
[-0.38115331, 0.31710028, 0.54375497],
[-0.4512085 , 0.71472175, 0.59512785]])pca_components = pca.components_
pca_table = pd.DataFrame(data=pca_components.T, columns=['PC1', 'PC2', 'PC3'])
pca_table.index = af_scaled.columns
pca_table
| PC1 | PC2 | PC3 | |
|---|---|---|---|
| danceability | 0.077096 | -0.206510 | -0.040335 |
| energy | 0.086123 | -0.457330 | -0.058991 |
| key | 0.163395 | -0.112386 | 0.977051 |
| loudness | 0.023853 | -0.140202 | -0.019456 |
| mode | -0.967991 | -0.203437 | 0.137496 |
| speechiness | 0.035025 | -0.033611 | -0.018382 |
| acousticness | -0.126278 | 0.719213 | 0.142816 |
| instrumentalness | -0.012401 | 0.107235 | 0.004570 |
| liveness | -0.000693 | -0.040947 | 0.002025 |
| valence | 0.070698 | -0.369037 | 0.012603 |
| tempo | 0.006319 | -0.082272 | -0.007944 |
# 기존 데이터를 주성분으로 표현한 새로운 Dafaframe 정의
af_pca_2 = pd.DataFrame(pca.fit_transform(af_scaled))
af_pca_2.columns = ['PC1', 'PC2', 'PC3']
af_pca_2
| PC1 | PC2 | PC3 | |
|---|---|---|---|
| 0 | 0.530326 | 0.140874 | -0.483661 |
| 1 | 0.569940 | 0.492794 | 0.220729 |
| 2 | -0.326235 | -0.175754 | 0.209222 |
| 3 | -0.347109 | 0.069145 | 0.400874 |
| 4 | -0.418030 | -0.127572 | -0.364484 |
| ... | ... | ... | ... |
| 20161 | -0.412399 | -0.064598 | -0.254455 |
| 20162 | -0.469749 | 0.774749 | 0.511434 |
| 20163 | 0.624897 | 0.404077 | 0.499165 |
| 20164 | -0.381153 | 0.317100 | 0.543755 |
| 20165 | -0.451208 | 0.714722 | 0.595128 |
20166 rows × 3 columns
k-means clustering
from sklearn.cluster import KMeans
from yellowbrick.cluster import KElbowVisualizer
plt.figure(figsize=(15,8))
visualizer = KElbowVisualizer(KMeans(init='k-means++', random_state=10), k=(2,15), timings=False)
visualizer.fit(af_pca_2)
visualizer.show()
km_pca_2 = KMeans(n_clusters=6, random_state=10)
km_pca_2.fit(af_pca_2)
KMeans(n_clusters=6, random_state=10)pred=km_pca_2.labels_
clust_pca_2 = af_pca_2.copy()
clust_pca_2['clust'] = pred
clust_pca_2.head()
| PC1 | PC2 | PC3 | clust | |
|---|---|---|---|---|
| 0 | 0.530326 | 0.140874 | -0.483661 | 4 |
| 1 | 0.569940 | 0.492794 | 0.220729 | 5 |
| 2 | -0.326235 | -0.175754 | 0.209222 | 3 |
| 3 | -0.347109 | 0.069145 | 0.400874 | 3 |
| 4 | -0.418030 | -0.127572 | -0.364484 | 1 |
clust_pca_2['clust'].value_counts()
3 5153
1 4366
0 3181
4 3131
2 3011
5 1324
Name: clust, dtype: int64visualizer = SilhouetteVisualizer(km_pca_2, colors='yellowbrick')
visualizer.fit(af_pca_2)
visualizer.show()
print("평균 실루엣 계수 =",visualizer.silhouette_score_)
평균 실루엣 계수 = 0.44327921127276076
Cluster별 시각화
data_cluster_2 = pd.concat([data.iloc[:, :3].reset_index(drop=True), clust_pca_2.reset_index(drop=True)], axis=1)
data_cluster_2.columns = ['id', 'url', 'Artist']+list(clust_pca_2.columns)
data_cluster_2
| id | url | Artist | PC1 | PC2 | PC3 | clust | |
|---|---|---|---|---|---|---|---|
| 0 | 0eFMbKCRw8KByXyWBw8WO7 | https://open.spotify.com/track/0eFMbKCRw8KByXy... | Jung Kook | 0.530326 | 0.140874 | -0.483661 | 4 |
| 1 | 7eJMfftS33KTjuF7lTsMCx | https://open.spotify.com/track/7eJMfftS33KTjuF... | Powfu | 0.569940 | 0.492794 | 0.220729 | 5 |
| 2 | 2CbGuO0LtVvbh3umN3mDwM | https://open.spotify.com/track/2CbGuO0LtVvbh3u... | Fujii Kaze | -0.326235 | -0.175754 | 0.209222 | 3 |
| 3 | 1JRNrJKTQhfvxII8kkIcAQ | https://open.spotify.com/track/1JRNrJKTQhfvxII... | Fujii Kaze | -0.347109 | 0.069145 | 0.400874 | 3 |
| 4 | 57u1FaZlztApkcT5x5XNuD | https://open.spotify.com/track/57u1FaZlztApkcT... | Fujii Kaze | -0.418030 | -0.127572 | -0.364484 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 20161 | 1AJZ9OpSs6V1jzUqdkdWPf | https://open.spotify.com/track/1AJZ9OpSs6V1jzU... | Various Artists | -0.412399 | -0.064598 | -0.254455 | 1 |
| 20162 | 3Q5c8dpE2aYMx97WnwRFGj | https://open.spotify.com/track/3Q5c8dpE2aYMx97... | Various Artists | -0.469749 | 0.774749 | 0.511434 | 2 |
| 20163 | 7aObrOB2jVZJ2vJ79lQGjU | https://open.spotify.com/track/7aObrOB2jVZJ2vJ... | Various Artists | 0.624897 | 0.404077 | 0.499165 | 5 |
| 20164 | 7MlsUrIhUPvjoLZhjTLfFo | https://open.spotify.com/track/7MlsUrIhUPvjoLZ... | Various Artists | -0.381153 | 0.317100 | 0.543755 | 2 |
| 20165 | 1FCbI6KSLpCu2lyu1hUwSO | https://open.spotify.com/track/1FCbI6KSLpCu2ly... | Various Artists | -0.451208 | 0.714722 | 0.595128 | 2 |
20166 rows × 7 columns
spotify_2 = af_cluster_2.groupby("clust").mean()
spotify_2
| danceability | energy | key | loudness | mode | speechiness | acousticness | instrumentalness | liveness | valence | tempo | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| clust | |||||||||||
| 0 | 0.700594 | 0.700649 | 8.960390 | -6.048014 | 0.0 | 0.132190 | 0.179351 | 0.029431 | 0.186324 | 0.587233 | 123.290654 |
| 1 | 0.656358 | 0.672687 | 1.317682 | -6.207548 | 1.0 | 0.114794 | 0.187537 | 0.033152 | 0.194695 | 0.523302 | 124.257614 |
| 2 | 0.494049 | 0.335678 | 4.807041 | -11.027916 | 1.0 | 0.065730 | 0.759359 | 0.088435 | 0.163378 | 0.316655 | 111.949661 |
| 3 | 0.649811 | 0.678134 | 8.007957 | -6.293207 | 1.0 | 0.102095 | 0.205783 | 0.024040 | 0.192048 | 0.559574 | 124.240705 |
| 4 | 0.685470 | 0.667810 | 2.878314 | -6.303537 | 0.0 | 0.129621 | 0.190217 | 0.023849 | 0.186051 | 0.524286 | 122.549215 |
| 5 | 0.552109 | 0.416870 | 5.816465 | -10.246002 | 0.0 | 0.109539 | 0.679766 | 0.106428 | 0.165272 | 0.351782 | 112.701530 |
scaler = MinMaxScaler()
spotify_2 = scaler.fit_transform(spotify_2)
spotify_2 = pd.DataFrame(spotify_2)
spotify_2.columns = ['danceability', 'energy', 'key', 'loudness', 'mode', 'speechiness',
'acousticness', 'instrumentalness', 'liveness', 'valence', 'tempo']
spotify_2
spotify_2=spotify_2.T
spotify_2.rename(columns = {'index':'Properties',0:'Cluster1',1:'Cluster2',2:'Cluster3',3:'Cluster4',4:'Cluster5',5:'Cluster6'}, inplace = True)
spotify_2
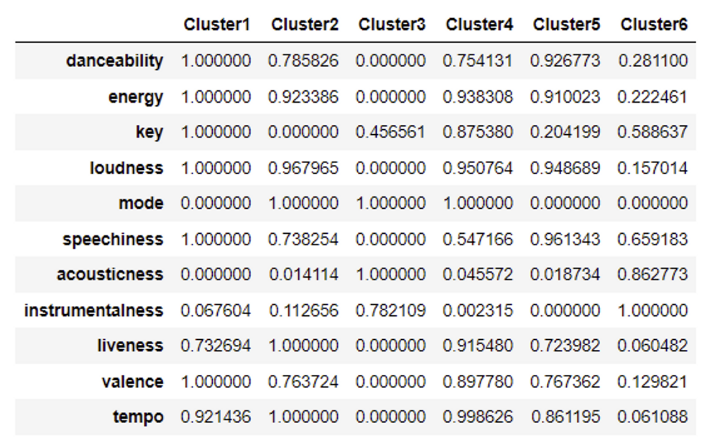
| Cluster1 | Cluster2 | Cluster3 | Cluster4 | Cluster5 | Cluster6 | |
|---|---|---|---|---|---|---|
| danceability | 1.000000 | 0.785826 | 0.000000 | 0.754131 | 0.926773 | 0.281100 |
| energy | 1.000000 | 0.923386 | 0.000000 | 0.938308 | 0.910023 | 0.222461 |
| key | 1.000000 | 0.000000 | 0.456561 | 0.875380 | 0.204199 | 0.588637 |
| loudness | 1.000000 | 0.967965 | 0.000000 | 0.950764 | 0.948689 | 0.157014 |
| mode | 0.000000 | 1.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 |
| speechiness | 1.000000 | 0.738254 | 0.000000 | 0.547166 | 0.961343 | 0.659183 |
| acousticness | 0.000000 | 0.014114 | 1.000000 | 0.045572 | 0.018734 | 0.862773 |
| instrumentalness | 0.067604 | 0.112656 | 0.782109 | 0.002315 | 0.000000 | 1.000000 |
| liveness | 0.732694 | 1.000000 | 0.000000 | 0.915480 | 0.723982 | 0.060482 |
| valence | 1.000000 | 0.763724 | 0.000000 | 0.897780 | 0.767362 | 0.129821 |
| tempo | 0.921436 | 1.000000 | 0.000000 | 0.998626 | 0.861195 | 0.061088 |
cluster 1 시각화
df = pd.DataFrame(dict(r=list(spotify_2['Cluster1']), theta=list(spotify_2.index)))
fig = px.line_polar(df, r='r', theta='theta', line_close=True,template="plotly_dark")
fig.update_traces(fill='toself')
fig.update_layout(
autosize=False,title_text="Radar Chart showing song Property in Cluster 1", title_x=0.5)
fig.show()
DMM
from sklearn.mixture import GaussianMixture
gm_bic= []
gm_score=[]
for i in range(2,11):
gm = GaussianMixture(n_components=i, n_init=10, tol=1e-3, max_iter=1000).fit(af_pca_2)
print("BIC for number of cluster(s) {}: {}".format(i, gm.bic(af_pca_2)))
print("Log-likelihood score for number of cluster(s) {}: {}".format(i, gm.score(af_pca_2)))
print("-"*100)
gm_bic.append(-gm.bic(af_pca_2))
gm_score.append(gm.score(af_pca_2))
BIC for number of cluster(s) 2: -87078.96389350256
Log-likelihood score for number of cluster(s) 2: 2.163723276954891
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 3: -93079.84639808125
Log-likelihood score for number of cluster(s) 3: 2.3149679471311337
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 4: -95600.97562800678
Log-likelihood score for number of cluster(s) 4: 2.3799348905729434
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 5: -97143.21347643886
Log-likelihood score for number of cluster(s) 5: 2.4206309974211435
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 6: -99032.26517192119
Log-likelihood score for number of cluster(s) 6: 2.4699260789557034
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 7: -99912.85726871144
Log-likelihood score for number of cluster(s) 7: 2.494217203367083
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 8: -100942.65117665297
Log-likelihood score for number of cluster(s) 8: 2.522207668529016
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 9: -101253.27984888543
Log-likelihood score for number of cluster(s) 9: 2.532367001197914
----------------------------------------------------------------------------------------------------
BIC for number of cluster(s) 10: -101504.51193904223
Log-likelihood score for number of cluster(s) 10: 2.541053642652003
----------------------------------------------------------------------------------------------------
gm_pca_2 = GaussianMixture(n_components=6, n_init=10, tol=1e-3, max_iter=1000).fit(af_pca_2)
pred=gm_pca_2.predict(af_pca_2)
clust_pca_2 = af_pca_2.copy()
clust_pca_2['clust'] = pred
clust_pca_2.head()
| PC1 | PC2 | PC3 | clust | |
|---|---|---|---|---|
| 0 | 0.530326 | 0.140874 | -0.483661 | 5 |
| 1 | 0.569940 | 0.492794 | 0.220729 | 4 |
| 2 | -0.326235 | -0.175754 | 0.209222 | 2 |
| 3 | -0.347109 | 0.069145 | 0.400874 | 3 |
| 4 | -0.418030 | -0.127572 | -0.364484 | 0 |
clust_pca_2['clust'].value_counts()
2 5266
5 4151
0 4036
3 3228
1 2005
4 1480
Name: clust, dtype: int64
Reference
[Clustering]
https://bangu4.tistory.com/98
https://saint-swithins-day.tistory.com/81
https://daebaq27.tistory.com/49
https://studying-haeung.tistory.com/14
https://steadiness-193.tistory.com/283
[GMM]
https://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture.bic
https://yeong-jin-data-blog.tistory.com/entry/GMM-Gaussian-Mixture-Models
[Scaling]
https://syj9700.tistory.com/56
https://dacon.io/codeshare/4526
https://mkjjo.github.io/python/2019/01/10/scaler.html
https://www.linkedin.com/advice/1/what-pros-cons-different-scaling-methods-data-normalization
[t-SNE]
https://jimmy-ai.tistory.com/126
https://bigdatamaster.tistory.com/186
https://skyeong.net/284
https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding
'deep daiv. > 추천시스템 project' 카테고리의 다른 글
| [text 감정 추출 모델] SVM 모델 학습 / text 감정 추출 결과 (0) | 2024.01.08 |
|---|---|
| [text 감정 추출 모델] Data Augmentation 데이터 증강 (0) | 2024.01.06 |
| [text 감정 추출 모델] 텍스트 전처리 / Goolgetrans 번역 API (0) | 2023.09.18 |
| [Audio feature 군집화] K-means 분류 모델 (0) | 2023.09.10 |
| [데이터 수집] 도서 데이터, 카카오 API (0) | 2023.09.05 |




