working_helen
[Audio feature 군집화] K-means 분류 모델 본문
Audio feature 군집화 과정에서 사용한 K-means 분류 모델에 대해 공부해본다.
1. K-means
1) K-means clustering
2) 분류 과정
3) 군집 개수 k 정하기
4) 초기 중심점 정하기
5) 분류 vs 군집화
6) 장점/단점
2. 성능 확인
1) 내부 평가 vs 외부 평가
2) silhouette score
3. 파이썬 코드
1. K-means
1) K-means clustering

(위키백과) k-평균 알고리즘(K-means clustering algorithm)은 주어진 데이터를 k개의 클러스터로 묶는 알고리즘으로, 각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작한다. 입력 데이터를 n보다 작거나 같은 k개의 그룹으로 나누는데, 이 때 각 그룹은 클러스터를 형성하게 된다. 다시 말해, 데이터를 한 개 이상의 데이터 오브젝트로 구성된 k개의 그룹으로 나누는 것이다.
각 그룹의 중심 (centroid)과 그룹 내의 데이터 오브젝트와의 거리의 제곱합을 비용 함수로 정하고, 이 함수값을 최소화하는 방향으로 각 데이터 오브젝트의 소속 그룹을 업데이트 해 줌으로써 클러스터링을 수행하게 된다.
- 데이터를 k개의 군집(cluster)로 구분하는 비지도 학습 알고리
- cluster : 유사한 특성을 가진 데이터 집단
centroid (Center of Cluster) : 각 클러스터의 중심
- 서로 유사한 특성을 가진 데이터끼리 같은 cluster에 속하게 된다.
- 클러스터 중심으로부터 각 데이터까지 거리의 분산을 최소로하는 k개의 centroid을 잡는다.
- 비용함수 = 각 centroid와 클러스터 내 데이터 간 거리의 제곱합
2) 분류 과정

step 1. 군집의 개수 k 결정
step 2. 초기 중심점 설정 : k개의 초기 centroid 설정
step 3. 데이터를 k개의 군집으로 분류하기 : 가장 가까운 중심점의 그룹에 속
step 4. centroid 갱신 : 해당 클러스터 내 데이터들의 평균 지점으로 업데이트
step 5. 더 이상 centroid의 이동이 없을 때까지 step 3와 4를 반복
3) 군집 개수 k 정하기
- Rule of thumb : 데이터 수가 n개일 때
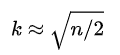

- Elbow Method
: 클러스터의 수를 하나씩 늘리면서 elbow point를 찾는 방식. 클러스터 1개를 추가했을 때 이전보다 크게 더 나은 결과를 나타내지 않는다면, 이전 클러스터의 수를 k로 설정한다.
- 클러스터 내 제곱합(SSW, Sum of Squares Within) = 각 데이터와 해당 클러스터 중심점과의 거리를 제곱한 값을 모두 합한 값
- elbow point = SSW 값의 그래프에서 급격한 감소가 더 이상 일어나지 않는 지점
4) 초기 중심점 정하기
- Randomly Partition
: 각 데이터들을 임의의 클러스터에 배당하는 무작위 분할 알고리즘
- K-means++
: 초기 중심점이 랜덤으로 선택되는 것의 단점을 개선하기 위해 사용되는 중심점 설정 방법
- step 1. 가지고 있는 데이터 중에서 무작위로 1개를 선택하여 첫번째 중심점으로 지정한다.
- step 2. 나머지 데이터들에 대해 해당 첫 중심점까지의 거리를 계산한다.
- step 3. step 2에서 계산한 거리에 비례하는 확률값을 기준으로 두번째 중심점을 정한다. 즉 이미 지정된 중심점으로부터 거리가 먼 데이터를 더 높은 확률로 다음 중심점으로 삼는다. 즉 centroid1을 두고, 이와 가장 멀리 떨어져 있는 데이터를 centroid2로 두고, centroid1과 2에서 가장 멀리 떨어져 있는 데이터를 centroid3으로 둔다.
- 중심점이 k개가 될 때까지 step 2와 3을 반복한다.
5) 분류 vs 군집화
- 분류
: 지도학습 알고리즘. 주어진 정답 label을 기반으로 데이터를 분류하는 기준을 학습하는 방식이다. 모델의 성능을 평가하기 위해 모델이 예측한 label과 실제 label을 비교하여 정확도를 확인한다. - 군집화
: 비지도 학습 알고리즘. 정답 label이 주어지지 않은 상태에서 데이터의 특성을 바탕으로 그룹화하는 방식이다. 각 그룹마다 그룹 내 데이터가 얼마나 동질적이고, 그룹 간에는 얼마나 이질적인지 확인함으로써 군집화의 유의미성을 판단한다. - 참고) 서로 유사해보이지만, K-NN은 분류 알고리즘이고 K-means은 군집화 알고리즘이다.
6) 한계점
- 분류 결과가 클러스터 개수 k값에 따라 크게 달라진다.
: k값이 무엇이냐에 따라 클러스터링의 결과가 크게 달라지며, 좋지 못한 결과를 보여줄 가능성도 있다. - 초기 중심점 위치에 따라 비용함수가 지역 최솟값으로 수렴할 수 있다.
: 초기 중심점을 어떻게 설정하느냐에 따라 비용 함수가 에러가 줄어드는 방향으로 최적화하는 과정에서 전역 최적값(global optimum)이 아닌 지역 최적값 (local optimum)으로 빠질 수 있다. - 이상치(outlier)에 민감하다.
: 중심점을 갱신하는 과정에서 이상값이 클러스터 내의 전체 평균 값을 왜곡시킴으로써 클러스터의 중심점이 클러스터의 실제 중심에 있지 않고 이상값 방향으로 치우치도록 만들 수 있다. - 구형이 아닌 데이터 분포에선 적절하지 않다.
: 유클리드 거리를 이용해 중심점과 각 데이터 간 거리를 계산하기 때문에 구형 형태의 군집이 형성된다. 따라서 데이터 분포가 구형이 아닌 경우 구형 클러스터로 군집화하기 부적절할 수 있다.
2. 성능 확인
1) 내부 평가 방식 vs 외부 평가 방식
- 내부 평가 (internal evaluation) : 데이터의 클러스터링한 결과에 대해서 클러스터 내 유사도가 높고, 클러스터 간 유사도가 낮은 (이질성이 높은) 경우 더 높은 점수를 주는 평가 방식. 데이터를 클러스터링한 결과물만을 보고 판단하여 내부 평가라고 불린다.
- 외부 평가 (external evaluation) : 클러스터링의 결과를 외부적으로 미리 정해진 결과물과의 비교로 평가하는 방식. 전문가의 의한 모범 결과, 외부 평가 기준 등을 이용해 클러스터링의 정확도를 평가한다.
2) silhouette score 실루엣 계수
- 실루엣 계수(실루엣 점수)를 계산해 클러스터 집합의 적합도를 측정
- k 개수 결정이나 클러스터링 기법 선택의 기준으로 사용
- 클러스터 내 거리(데이터 간 거리) + 클러스터 간 거리를 모두 고려
=> 클러스터 내 거리가 얼마나 작은지 + 클러스터 간 간격이 적당한지 (각 클러스터가 여유로운 거리로 구분되고 있는지)
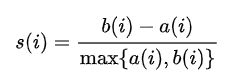
- a_i = 평균 클러스터 내 거리 = 데이터 i가 속한 클러스터 내부의 다른 데이터들과의 부동성
- b_i = 평균 클러스터 간 거리 = 데이터 i가 속하지 않은 클러스터의 데이터들과의 부동성
- s_i = 데이터 i의 실루엣 계수, 1 <= s_i <= 1
- s_i가 1에 가까울수록 i가 올바른 클러스터에 분류되었음을 의미
- s_i가 -1에 가까울수록 i가 잘못된 클러스터에 분류되었음을 의미. 데이터가 이웃 클러스터에 더 가까워 아예 잘못 할당된 상태를 의미
- s_i가 0에 가까운 것은 두 군집 간 거리가 거의 비슷한 경우를 의미하며, 군집이 잘 구분되지 않은 상태를 의미
from sklearn.metrics import silhouette_samples, silhouette_score
# 각 데이터의 실루엣 계수
score_samples = silhouette_samples(data, label, metric='euclidean')
irisDF['silhoutte_coeff'] = score_samples
# 각 클러스터의 평균 실루엣 계수
irisDF.groupby('cluster')['silhoutte_coeff'].mean()
# 전체 데이터의 평균 실루엣 계수
average_score = silhouette_score(data, label, metric='euclidean')- silhouette_samples : 데이터 set과 군집 레이블 값(label)를 입력 → 각 데이터 포인트의 실루엣 계수 반환
- silhouette_score : 데이터 set과 군집 레이블 값(label)를 입력 → 전체 데이터의 평균 실루엣 계수 반환
- 전체 데이터의 평균 실루엣 계수 값이 크고, 클러스터별 평균 실루엣 계수 값이 클수록 좋다.
# 실루엣 계수 시각화
from yellowbrick.cluster import SilhouetteVisualizer
visualizer = SilhouetteVisualizer(kmeans 모델, colors='yellowbrick')
visualizer.fit(df)
visualizer.show()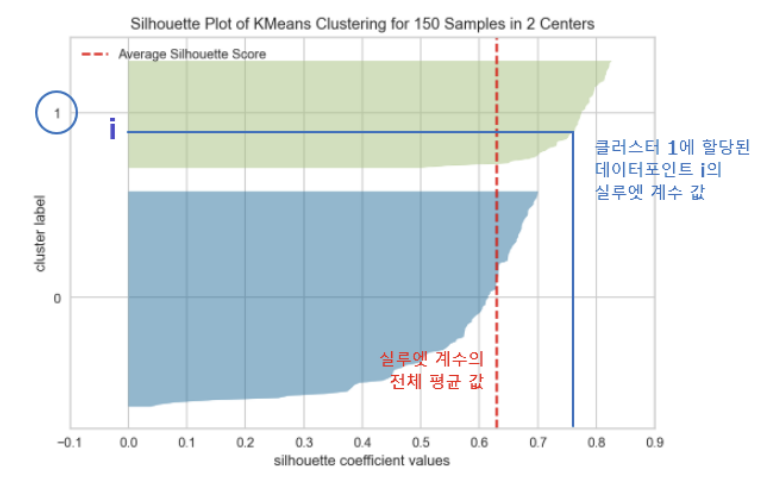
- SilhouetteVisualizer : 실루엣 계수 시각화
- y축 : 클러스터 번호
- x축 : 실루엣 계수
- 색 부분 : 각 클러스터에 속하는 데이터별 실루엣 계수값 내림차순
- 빨간 점선 : 실루엣 계수의 전체 평균값
- 실루엣 계수는 그 값을 시각화할 수 있다는 장점이 있다.
- 클러스터 내의 데이터의 실루엣 계수가 1에 가까울수록, 전체적인 값이 급격히 감소하지 않을수록 좋다.
3. 파이썬 코드
- 모델 학습
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters, random_state, init = 'k-means++', max_iter)
kmeans.fit(df)- n_clusters : 클러스터 개수 지정
- random_state : randomseed 값
- init : 초기 Centroid를 정하는 방법. default가 k-means++이고, 'random'으로 설정하면 무작위로 설정.
- max_iter : 갱신의 최대 반복 횟수로 이 횟수 이전에 중심점 갱신이 없으면 종료. default는 300
-학습 결과 확인
kmeans.labels_ : 각 데이터가 분류된 군집의 label
kmeans.cluster_centers_ : 각 군집의 중심점 좌표
kmeans.inertia_ : 모델의 손실 함수값 = 중심과의 거리 제곱합
kmeans.predict(X) : 새로운 input X에 대한 군집화- inertia : 중심점과의 거리를 제곱합 SSW를 반환
= 클러스터 내 데이터가 얼마나 밀접하게 모여 있는지를 나타내며, 클러스터 내 분산의 측도이다.
K-means 알고리즘이 최적의 클러스터 개수를 찾는 데 사용되는 elbow method에서는 k개수에 따른 각 모델의 inertia가 계산되어 그래프로 그려진다. 이 그래프에서 클러스터 개수가 증가함에 따라 inertia가 줄어드는데, 클러스터 개수가 증가할수록 inertia가 줄어드는 폭이 감소한다. 이 감소폭을 기준으로 elbow point를 찾을 수 있다.
- elbow method
from yellowbrick.cluster import KElbowVisualizer
visualizer = KElbowVisualizer(kmeans 모델, k=(min, max), metric='silhouette', timings=False)
visualizer.fit(df)
visualizer.show()- k = (min, max) : 확인해볼 k값 범위
- timings : 각 k마다 모델 fitting 시간을 표시, default = True
- distance_metric : 데이터 간 거리를 계산할 때 기준 함수 지정, default = 'euclidean'
- metric : 모델을 평가하는 평가함수 지정, default = 'distortion'
- distortion : centroid까지 거리 제곱의 평균
- silhouette : 실루엣 계수 값
- 분류 결과 시각화 (k = 3일때 예시)
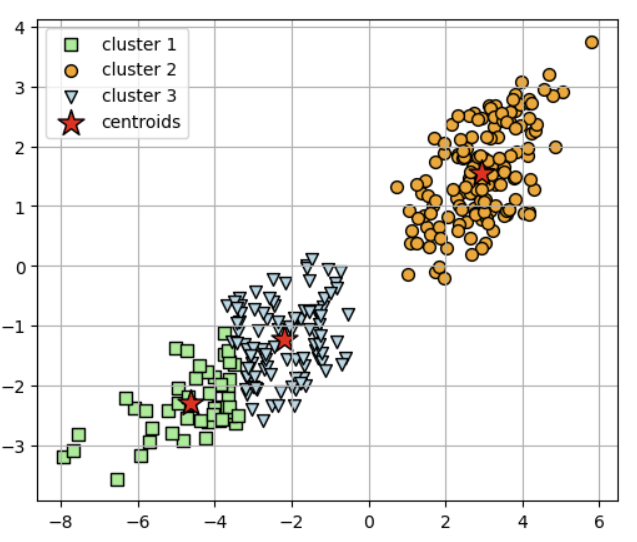
plt.figure(figsize=(6,4))
#y=0으로 분류된 af
plt.scatter(af_scaled[y_km == 0, 0], af_scaled[y_km == 0, 1],
s=50, c='lightgreen', marker='s', edgecolor='black', label='cluster 1')
#y=1로 분류된 af
plt.scatter(af_scaled[y_km == 1, 0], af_scaled[y_km == 1, 1],
s=50, c='orange', marker='o', edgecolor='black', label='cluster 2')
#y=2로 분류된 af
plt.scatter(af_scaled[y_km == 2, 0], af_scaled[y_km == 2, 1],
s=50, c='lightblue', marker='v', edgecolor='black', label='cluster 3')
#각 클러스터의 중심점 좌표
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', edgecolor='black', label='centroids')
plt.legend(scatterpoints=1)
plt.show()
- feature가 많은 경우 시각화
PCA → 3개의 PC를 이용해 3차원에서 시각화
PCA → 2개의 PC를 이용해 2차원에서 시각화
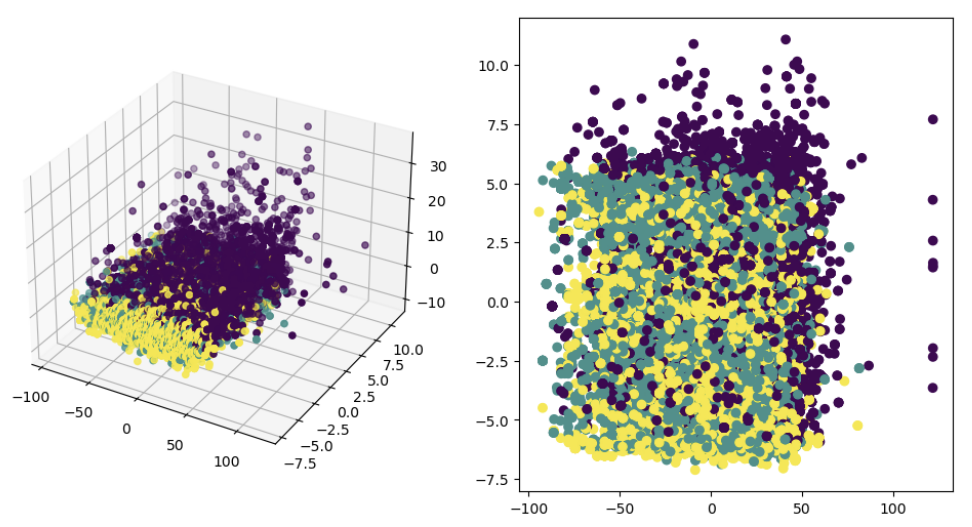
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
# 3차원으로
df_reduced = PCA(n_components = 3).fit_transform(df)
results =pd.DataFrame(df_reduced, columns=['pca1','pca2', 'pca3'])
fig = plt.figure(figsize=(12, 6))
plt.suptitle('K-means Clustering with 3 dimensions')
ax = fig.add_subplot(121, projection='3d')
ax.scatter('pca1','pca2', 'pca3', data=results, c=np.array(list(df['clust'])))
# 2차원으로
df_reduced = PCA(n_components = 2).fit_transform(df)
results =pd.DataFrame(df_reduced, columns=['pca1','pca2'])
plt.suptitle('K-means Clustering with 2 dimensions')
ax2 = fig.add_subplot(122)
ax2.scatter(x="pca1_2", y="pca2_2", data=results, c=np.array(list(df['clust'])))
Reference
https://ko.wikipedia.org/wiki/K-%ED%8F%89%EA%B7%A0_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://waterprogramming.wordpress.com/tag/k-means/
https://velog.io/@jhlee508/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-K-%ED%8F%89%EA%B7%A0K-Means-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://itstory1592.tistory.com/19
https://dacon.io/codeshare/5776
https://velog.io/@khsfun0312/K-means-Clustering
https://planharry.tistory.com/43
https://csshark.tistory.com/110
https://studying-haeung.tistory.com/13
https://www.scikit-yb.org/en/latest/api/cluster/elbow.html
https://datascience.stackexchange.com/questions/48693/perform-k-means-clustering-over-multiple-columns
https://codetorial.net/matplotlib/3d_scatter_plot.html
'deep daiv. > 추천시스템 project' 카테고리의 다른 글
| [text 감정 추출 모델] SVM 모델 학습 / text 감정 추출 결과 (0) | 2024.01.08 |
|---|---|
| [text 감정 추출 모델] Data Augmentation 데이터 증강 (0) | 2024.01.06 |
| [text 감정 추출 모델] 텍스트 전처리 / Goolgetrans 번역 API (0) | 2023.09.18 |
| [Audio feature 군집화] Spotify Song Clustering with k-means (0) | 2023.09.16 |
| [데이터 수집] 도서 데이터, 카카오 API (0) | 2023.09.05 |




