working_helen
[추천시스템 논문 리뷰] 4주차 : Loss function 본문
논문 리뷰를 바탕으로 Factorization model을 구현해보는 과정에서 학습한 loss function에 대해 정리해본다.
1. Loss function
1) loss fuction 손실 함수
2) 모델의 학습
3) loss function 종류
2. 회귀모델 loss function
1) 평균제곱오차 MSE
2) 평균제곱근오차 RMSE
3) 평균절대오차 MAE
3. 분류모델 loss function
1) 분류 문제의 종류
2) Activation Function
3) entropy
4) Cross entropy
5) Binary Cross entropy
6) Categorical Cross entropy
7) Sparse categorical cross entropy
1. Loss function
1) loss fuction 손실 함수
loss 손실 = 머신러닝 혹은 딥러닝 모델이 제시하는 출력값 y_hat과 정답값 y 사이 오차
loss function = loss 점수를 계산하는 함수 = 출력값 y_hat과 정답값 y의 차이를 표현하는 지표
Optimization 최적화 = loss function 함숫값이 최소가 되는 파라미터를 찾는 과정
- loss function 함숫값이 커질수록 오차가 커져 좋지 않은 모델이 된다.
- 모델은 최적화 과정을 통해 loss function 함수값이 최소화하는 파라미터를 찾기 위해 학습 과정을 진행한다.
- f1 score, precision 등의 모델 성능 지표는 학습 이후 모델의 최종 성능을 평가하는 지표인 반면, loss function은 모델의 학습 과정에서 얼마나 학습이 잘 되고 있는지 평가하는 지표라는 점에서 엄연한 차이가 있다.
2) 모델의 학습

- L : loss function
- argmin: arguments of minimum, L을 최소화하는 입력값을 찾음
- x : 학습 데이터 입력값
- y : 학습 데이터 정답값
- θ : 모델 학습 시 사용되는 파라미터의 벡터
- θ_hat : 추정된 최적의 파라미터
모델이 학습한다 = 모델 예측값과 정답값 사이의 차이를 최소화하는 파라미터 θ를 찾는다
= loss function 값을 최소화하는 파라미터 θ를 찾는다
3) loss function 종류
회귀 모델 loss function : MSE, MAE, RMES 등
분류 모델 loss function : Binary cross-entropy, Categorical cross-entropy 등
평균제곱오차(MSE)와 교차 엔트로피 오차(cross entropy error)를 주로 사용한다.
2. 회귀모델 loss function
1) 평균제곱오차 MSE (Mean Squared Error)

- 오차 제곱 합의 평균
- MSE 값이 작을수록 오차가 적어 모델의 성능이 더 좋다.
- 제곱 연산으로 인해 오차가 커질수록 loss function 값이 빠르게 증가한다.
- 제곱을 사용하기 때문에 절댓값이 1미만인 오차는 더 작아지고, 1보다 큰 오차은 더 커지는 왜곡이 존재한다.
- 제곱을 사용하기 때문에 outlier의 오차를 줄였을때 전체 loss function 값이 많이 감소할 수 있으므로 outlier에 민감하다.즉 전체 loss를 감소하기 위해 outlier의 오차를 줄이는데 집중하며 특이값의 영향을 많이 받게된다.
2) 평균제곱근오차 RMSE (Root Mean Squared Error)

- MSE에 루트(√)를 씌운 값
- RMSE 값이 작을수록 오차가 적어 모델의 성능이 더 좋다.
- MSE는 오차의 제곱으로 계산되기 때문에 실제 오차보다 스케일이 커진다. 따라서 MSE에 루트를 씌운 RMSE을 이용하면 오차값의 증가를 막고, y와 동일한 단위에서 오차를 해석할 수 있다.
3) 평균절대오차 MAE (Mean Absolute Error)
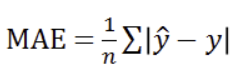
- 절대 오차 합의 평균
- MAE가 작을수록 오차가 적어 모델의 성능이 더 좋다.
- MSE와 달리 loss function 값이 오차에 비례하여 일정하게 증가한다.
- MSE에 비해 outlier에 robust하다. 모든 오차의 절댓값합의 평균이므로 outlier 1개의 오차를 줄이는 방향으로 학습하는 것과 outlier를 무시하고 다른 데이터들의 오차를 줄여 학습하는 것이 loss를 감소하는 측면에서 유사하다. 따라서 굳이 outlier의 오차를 줄이려고 하지 않고 오차가 유난히 큰 값은 무시하고 학습하기 때문에 outlier의 영향이 적다.
3. 분류모델 loss function
1) 분류 문제의 종류
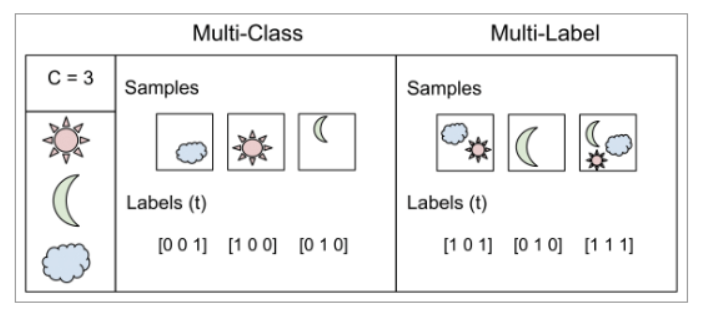
Multi-class classification : 각 샘플은 여러 클래스 항목 중 하나로 분류, 하나의 positive만 가짐
Multi-Label Classficiation : 각 샘플 여러 클래스 중 해당되는 클래스들로 레이블, 하나 이상의 positive를 가질 수 있음
2) Activation Function 활성화 함수
: 딥러닝 모델을 구축시 연산 layer 뒤에 사용되어 다음 층 뉴런을 활성화시킬지 결정하는 함수
연산 layer의 출력 노드값이 정해진 threshold보다 크면 통과시키고, 작으면 0을 출력해 다음 노드를 비활성화시킨다.
연산 방식, task 등에 따라 적절한 활성화 함수를 선택해야 한다.
- Sigmoid :출력값을 (0, 1) 사이 값으로 압축한다.
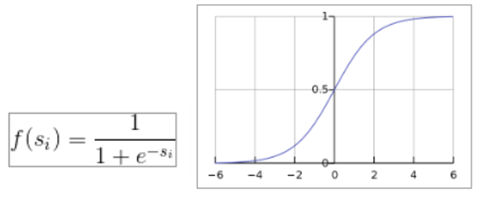
- Softmax : 각 클래스 벡터가 (0, 1) 범위에 속하고, 합이 1이 되도록 변환한다.
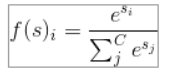
3) entropy 엔트로피
(위키백과) 정보 엔트로피는 각 메시지에 포함된 정보의 기댓값(평균)이다. 확률이 낮을수록, 어떤 정보일지는 불확실하게 되고, 우리는 이때 '정보가 많다', '엔트로피가 높다'고 표현한다. 어떤 사람이 정보를 더 많이 알수록 새롭게 알 수 있는 정보는 적어진다는 것이다. 어떤 사건의 확률이 매우 높다고 가정하자. 우리는 그 사건이 발생해도 별로 놀라지 않는다. 즉, 이 사건은 적은 정보를 제공한다. 반대로, 만약 사건이 불확실하다면, 그 사건이 일어났을 때 훨씬 유용한 정보를 제공한다. 그러므로, 정보량(information content)은 확률에 반비례한다.
- 불확실성 척도, 정보학에선 정보량의 기댓값을 의미한다.
- 정보의 발생확률이 적을수록 = 정보의 불확실성이 높을수록 = 정보의 엔트로피는 증가한다.
- 발생 확률이 높은 사건의 정보(= 누구나 알만한 일반적인 정보)의 엔트로피는 작고,
발생 확률이 적은 사건의 정보(= 새롭고 일반적이지 않은 정보)의 엔트로피는 크다.
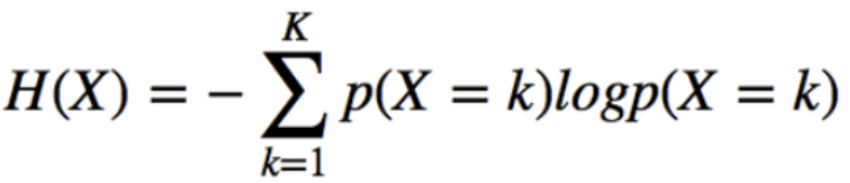
- 엔트로피 H(p) = 확률 변수 X의 확률 분포의 불확실성
- X가 특정한 값을 가질 확률이 1에 가까워질수록 = 불확실성이 감소할수록 = 엔트로피 값 H(p)는 작아진다.
반대로 X가 각 값을 가질 확률이 p(X=k) = 1/K로 유사할수록 = 불확실성이 커질수록 = 엔트로피 값 H(p)는 커진다.
4) 교차 엔트로피 Cross entropy (CE)
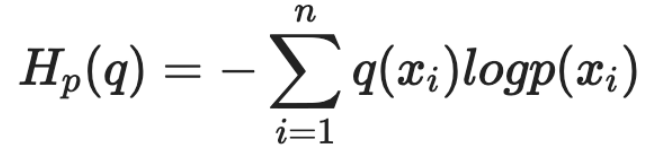
- 하나의 확률변수 X가 서로 다른 분포 p, q를 따르는 경우
두 확률분포가 얼마나 유사한지, 두 확률 분포의 차이를 나타내는 지표
- q = 실제 확률분포, 모델이 추정하고자 하는 미지의 확률분포
p = 예측 확률분포, 모델의 추정 확률분포
- 실제값과 예측값이 같은 경우 H(p, q)의 값이 0으로 수렴하고, 값이 커질수록 두 분포 간 차이가 커진다.
- 모델은 교차 엔트로피 값을 감소시키는 방향으로 예측분포 p를 실제분포 q에 근사한다.

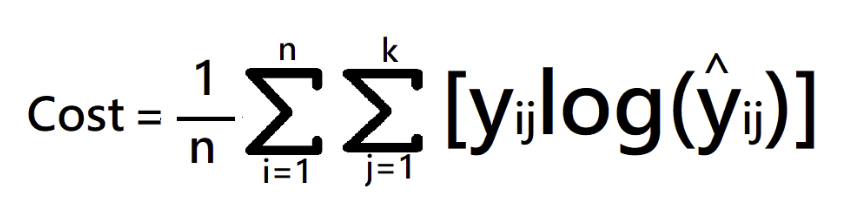
- 1개의 입력값마다, K개의 클래스를 대상으로 교차 엔트로피 계산
- n개의 교차 엔트로피 값의 평균으로 전체 모델의 loss 계산
5) Binary Cross entropy (log loss)
- 클래스가 0과 1인 Binary classification 모델에서 사용하는 교차 엔트로피
- 각 클래스에 대한 Binary classification을 진행함으로써 Multi-class classification에도 사용된다.
- 교차 엔트로피 값은 예측값 p(y_i)와 실제값 y_i이 유사할수록 0에 수렴하고, 두 값이 다를수록 양의 무한대로 커진다.
- 활성화 함수로 sigmoid 함수를 사용한다.
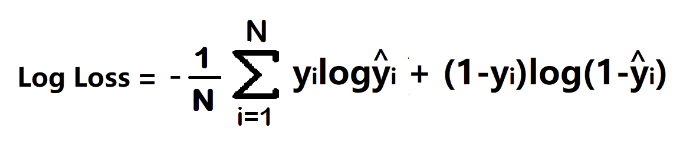
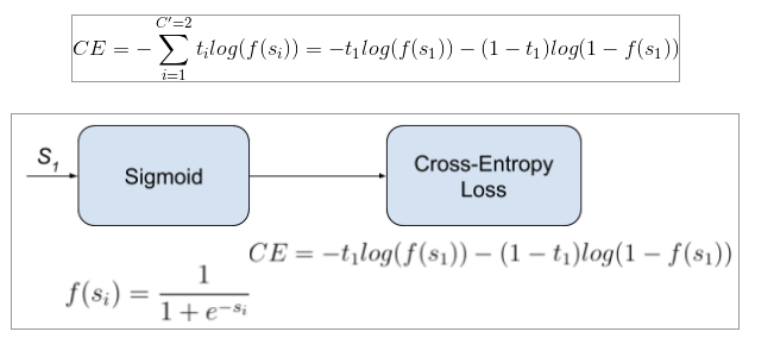
[변수 정리]
y_i = 정답값 / y_i_hat = i번째 입력에 대한 모델 예측값 / N = 전체 i 개수
t_i = 정답값 / f(s_i) : 각 클래스 i에 대한 예측값 N개의 평균 / C = 2 = 클래스 2개
6) Categorical Cross entropy
- 클래스가 3개 이상인 Multi-class classification 모델에서 사용하는 엔트로피
- 데이터의 label이 (0,0,1,0), (1,0,0,0)과 같이 one-hot encoding 상태에서 사용할 수 있다.
- 활성화 함수로 softmax를 사용한다.
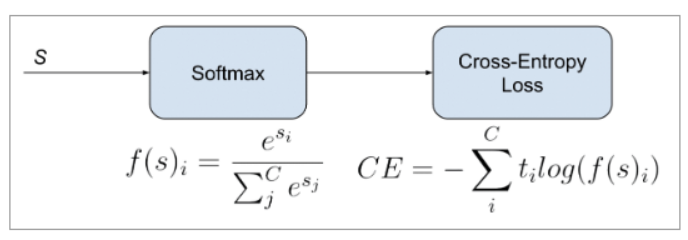
[변수 정리]
t_i = 정답값 / f(s_i) : 각 클래스 i에 대한 예측값 N개의 평균 / C = 클래스 개수
7) Sparse categorical cross entropy
- 클래스가 3개 이상인 Multi-class classification 모델에서 사용하는 엔트로피
- 데이터의 label이 (0,1,2,3)과 같이 정수 인코딩 상태에서 사용한다. 사전에 one-hot encoding된 상태로 변환해주지 않아도 정수로 된 label을 주면 내부적으로 알아서 one-hot vector로 변환해 계산한다. 따라서 이미 label이 one-hot vector 형태라면 Categorical Cross entropy를, 정수 인코딩 형태라면 Sparse Categorical Cross entropy를 사용하면 된다.
Reference
https://ko.wikipedia.org/wiki/%EC%A0%95%EB%B3%B4_%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BC
https://velog.io/@rcchun/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%86%90%EC%8B%A4%ED%95%A8%EC%88%98%EC%9D%98-%EC%A2%85%EB%A5%98
https://velog.io/@yuns_u/%EC%86%90%EC%8B%A4%ED%95%A8%EC%88%98-%EA%B0%84%EB%9E%B5-%EC%A0%95%EB%A6%AC
https://heytech.tistory.com/361
https://heytech.tistory.com/379
https://wordbe.tistory.com/entry/ML-Cross-entropyCategorical-Binary%EC%9D%98-%EC%9D%B4%ED%95%B4
https://yeong-jin-data-blog.tistory.com/entry/%EA%B5%90%EC%B0%A8-%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BCCross-Entropy
https://www.analyticsvidhya.com/blog/2022/06/understanding-loss-function-in-deep-learning/
https://jins-sw.tistory.com/16
'deep daiv. > 추천시스템 스터디' 카테고리의 다른 글
| [추천시스템 논문 리뷰] 5주차 : Neural Collaborative Filtering (0) | 2023.08.27 |
|---|---|
| [추천시스템 논문 리뷰] 5주차 : Matrix Factorization, Netflix (3) | 2023.08.27 |
| [추천시스템 논문 리뷰] 3주차 : 경사하강법 / SGD (0) | 2023.08.24 |
| [추천시스템 논문 리뷰] 3주차 : Factorization Machines (2) | 2023.08.23 |
| [추천시스템 논문 리뷰] 3주차 : SVM (0) | 2023.08.23 |





