working_helen
[추천시스템 논문 리뷰] 3주차 : Factorization Machines 본문
논문명 : Factorization Machines
저자명 : Steffen Rendle
팀명 : 시고르자브종
파일
본 논문에서는 Factorization Machines(FM) 모델에 대해 설명한 후, SVM(Support Vector Machines)과의 비교와 다른 factorization model로의 확대 가능성을 보임으로써 FM 모델의 장점을 보여주고자 한다.
✏️ 논문 내용 요약
1. FM은 SVM와 factorization model의 장점을 결합한 새로운 모델이다.
2. FM은 아래와 같은 장점이 있다.
- sparse data에도 적용가능하다.
- linear 방정식을 가지며, linear time 내에 연산이 가능하다.
- general predictor이다.
3. FM은 sparse data에서 SVM보다 더 효과적으로 적용될 수 있다.
4. FM은 input를 적절한 feacture vector 형태로 구성해주면 다양한 factorization model을 흉내낼 수 있다.
0. Abstract
- FM은 SVM과 factorization model의 장점을 합친 새로운 모델이다.
- FM은 SVM과 동일하게 general predictor이지만, SVM과 달리 sparse한 데이터에도 잘 적용될 수 있다.
- FM의 방정식은 linear time이다.
- FM은 MF, SVD++, PITF, FPMC 등 다양한 factorization model이 적용되는 문제에 사용될 수 있다.
※ general predictor
어느 실수 값 feature vector가 input값으로 들어와도 잘 작동하는 predictor
데이터의 형태에 크게 규제 받지 않고, 분류, 회귀 등 다양한 작업을 수행 할 수 있다.
1. Introduction
1) SVM의 문제점
: SVM은 머신러닝과 데이터 마이닝에서 가장 유명한 predictor 중 하나이지만, 협업 필터링 문제의 경우 SVM을 적용하기 어렵다. SVM이 매우 sparse한 데이터의 비선형적인 kernel 공간에서 reliabel parameter(hyperplane 초평면)를 학습할 수 없기 때문이다.
2) Factorization Model의 문제점
: 행렬/텐서 혹은 특수 factorization model들은 모델링 및 설계에 노력이 필요한 특이적이고 전문화된 작업으로부터 개별적으로 유도되었다. 이 때문에 general prediction 작업을 하지 못하며 특정 input값에 대해서만 제한적으로 작동할 수 있다.
3) FM의 장점
- FM은 SVM과 같이 general predictor이지만, SVM이 잘 적용되지 않는 매우 sparse한 데이터에도 적용될 수 있다.
이는 `dense parametrization`을 사용하는 SVM과 달리, FM이 `factorized parametrization`을 사용하여 변수들 사이의 상호작용을 모델링하기 때문이다.
- linear number의 파라미터를 가지며, linear time에 학습하기 때문에 즉각적인 최적화와 parameters 저장이 가능하다.
이와 달리 non-linear SVM은 daul form 최적화와 학습데이터 의존적인 예측 계산을 사용한다.
- FM은 general predictor임에도 input data를 적절히 정의함으로써 다양한 factorization model을 흉내낼 수 있다.
MF, SVD++, PITF, FPMC 등의 기존 factorization models은 협업 필터링 문제에 적용할 수 있지만 input data가 매우 제한적이라는 문제가 있었다.
➡️ FM = general predictor(SVM의 장점)+ sparsity에서도 적용(factorization models의 장점)
2. Prediction Under Sparsity
1) common prediction task
: 일반적으로 예측 문제는 feature vector x(∈ R^n)로부터 target 범위 T로 매핑하는 함수 y를 추정하는 것
function y : R^n →T
input 실수 값 공간 : R^n
target 값의 공간 : T
학습 데이터 : D = {(x(1), y(1)), (x(2), y(2)), . . .}
2) feature vector x가 highly sparse일때 prediction task
: 본 논문에서는 feature vector x의 성분 x_i가 대부분 0인 매우 sparse한 조건에서 prediction 문제를 해결하는데 FM을 사용할 수 있음을 보인다. 이러한 huge sparsity는 real-world 데이터에서 많이 발견되는데 그 이유 중 하나로 거대한 범주형 변수 도메인을 다룬다는 것이 있다.
m(x) : feature vector x에서 non-zero 원소들의 수
mD : 모든 feature vector x의 m(x) 평균
🎬 영화 리뷰 시스템의 거래 데이터에서 feature vectors 예시

U (user) : active user의 binary indicator variable
I (item) : active item의 binary indicator variable
R (rating) : 각 user가 평가한 적 있는 item
사용자가 평점을 매긴 모든 영화에 대해 총합이 1이 되도록 정규화
t (time) : Jan.2009을 1로 정의하여 month 단위로 시간 표현
Last rating : active movie 보기 직전에 봤던 last movie
target y : rating 값 (train 데이터에서 정답값, test 데이터에서 예측값)
Observed data example S
S = {(A, TI, 2010-1, 5), (A, NH, 2010-2, 3), (B, SW, 2009-5, 4), (B, ST, 2009-8, 5), (C, SW, 2009-12, 5), ,,, }
- U = {Alice (A), Bob (B), Charlie (C), . . .}
- I = {Titanic (TI), Notting Hill (NH), Star Wars (SW), Star Trek (ST), . . .}
(A, TI, 2010-1, 5) : 사용자 A가 영화 TI(titanic)의 평점을 2010년 1월에 5점으로 남겼다는 의미
3. Factorization Machines(FM)
A. Factorization Machine Model
1) 2-way FM (degree d = 2) 모델 방정식

w_0 : global bias
w_i : strength of the i-th variable = i번째 변수의 영향력
<v_i, v_j> : interaction between the ith and j-th variable = i번째 변수와 j번째 변수의 상호작용
📌 <v_i, v_j> = w_i,j 추정량
: FM은 w_i,j을 사용하지 않고 factorizing을 통해 얻은 w_i,j의 추정량을 사용한다. 이 원리는 FM이 sparse 데이터의 고차원 상호작용에 대해서 좋은 parameter 추정치를 산출할 수 있게 만드는데 중요한 역할을 한다.
2) 표현 방법
- k가 충분히 크면 positive definite 행렬 W에 대해 W = V∙Vt를 만족하는 행렬 V가 반드시 존재한다. 따라서 k가 충분히 크다면 FM는 어떠한 행렬 W도 표현할 수 있다.
- 그러나 데이터가 sparse 환경에서는 복잡한 상호작용을 추정할 충분한 정보가 없기 때문에 작은 k값을 선택해야 한다. k를 제한하는 것은 더 좋은 일반화로 이어지며 sparsity에서도 상호작용 행렬을 만들 수 있다.
3) Sparsity 상태에 파라미터 추정
- sparse 상태에서는 변수 간 상호작용을 directly하고 independently하게 추정할 충분한 데이터가 없다.
- 하지만 FM은 아래와 같은 이유로 sparse 상태에서도 상호작용을 잘 추정할 수 있다.
interaction parameters간 factorizing을 사용함으로써 독립성을 깨버린다.
= interaction parameters간 연관이 생기게 만든다.
= 하나의 interaction 데이터가 관련 있는 다른 interaction를 추정하는 데도 도움을 준다.
4) 계산
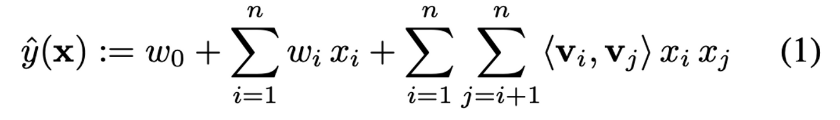
- 모든 pairwise interaction들을 계산해야하므로 방정식 (1)의 계산 복잡도는 O(k*n^2)이다.
- 하지만 아래와 같이 pairwise interaction 부분을 아래와 같이 재표현하면 계산 복잡도를 linear time으로 줄어든다.
- Lemma 3.1) FM의 모델 방정식은 linear time O(k*n)으로 계산할 수 있다.
: 아래 방정식의 복잡도는 O(k*n)으로 linear time이다. 이때 sparsity하에서는 대부분의 원소가 0이기 때문에 non-zero 원소들만 계산하므로 결국 FM의 계산 복잡도는 O(k*mD)이 된다.
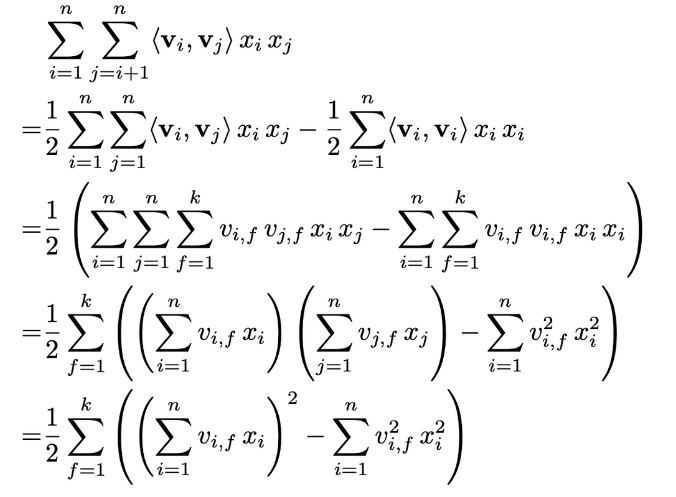
B. Factorization Machines as Predictors
: FM은 Regression, Binary classification, Ranking 등 다양한 예측 업무에서 적용할 수 있다.
이 모든 경우에서 오버피팅을 방지하기 위해 L2와 같은 정규화 term이 추가된다.
C. Learning Factorization Machines
: FM의 모델 파라미터(w_0, w_i, V)는 `gradient descent methods(경사하강법)`를 통해 효과적으로 학습할 수 있다.
FM의 gradient
일반적으로 각 gradient는 O(1)의 시간 내에 계산 가능하며, gradient 값을 기반으로 한 parameter 업데이트는 O(k*n) (혹은 O(k*m(x)) 시간 내에서 완료될 수 있다.
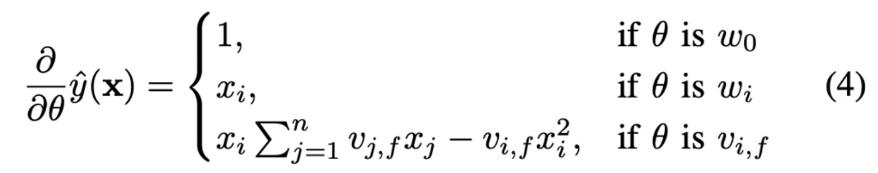
D. d-way Factorization Machine
: 2-way FM으로부터 d-way FM으로 쉽게 확장할 수 있다.
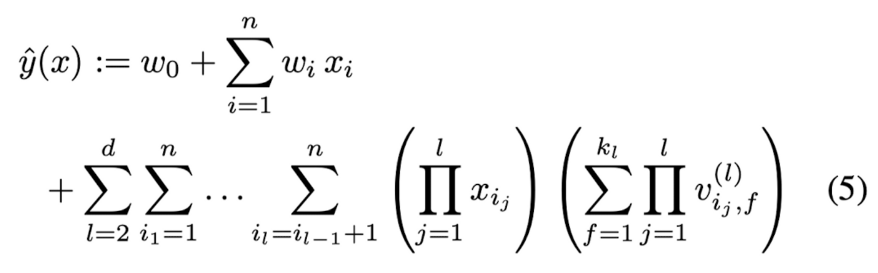
l번째 interaction 항에 대한 parameters는 PARAFAC(parallel factor analysis : 병렬분석) 모델로 factorize된다. 방적식 (5)의 복잡도는 O(k_d*n^d)이지만 유사하게 lemma 3.1을 적용하면 linear time으로 계산할 수 있다.
E. Summary
📌 `factorized parametrization`을 사용하는 FM은 factorizing으로 계산한 interaction을 사용하여 feature vector x 의 가능한 모든 상호작용을 모델화할 수 있다. 이 원리는 아래와 같은 이유로 FM이 sparse 데이터의 고차원 상호작용에 대해서 좋은 parameter 추정치를 산출할 수 있게 해준다.
- high sparsity에서 변수 사이의 상호작용을 추정할 수 있으며, 관찰되지 않은 상호작용에 대한 generalize(일반화)도 할 수 있다.
- 예측과 학습에 있어 parameter의 수만큼 linear time이 소요된다. 이 덕분에 SGD을 사용해 다양한 손실 함수에서 즉각적인 최적화가 가능하다.
3. FMs VS SVMs
: FM과 SVM의 원리를 분석하여 SVM에 비해 FM이 가지는 장점을 제시한다.
A. SVM model
SVM 모델 기본구조
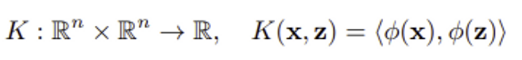
function y의 추정식 : yˆ(x) = <φ(x), w>
φ : feature space R로부터 complex space F로 매핑하는 함수
x : input ∈ R
w : model parameter ∈ F
1) Linear kernel
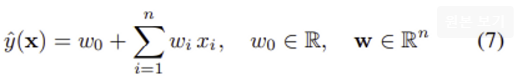
φ(x) := (1, x_1, . . . , x_n)
Linear kernel K_l(x, z) := 1 + <x, z>
2) Polynomial kernel
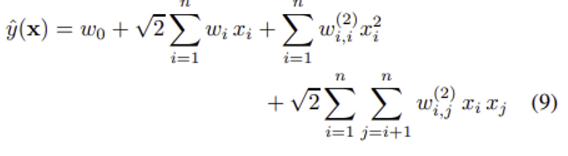
polynomial kernel K(x, z) := (<x, z> + 1)^d
w_0 ∈ R, w ∈ R^n
W^(2) ∈ R^n×n (symmetric matrix)
변수 간 고차원 interactions 항 w_i,j가 추가된다.
📌 polynomial kernel의 방정식 (9)와 FM의 방정식 (1) 비교
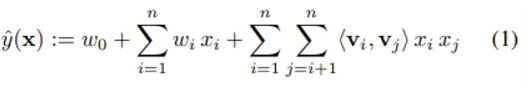
- SVM의 interaction parameters = w_i,j : 서로 completely independent하다.
- FM의 interaction parameters = <v_i, v_j> : 서로 의존적이며, parameter를 공유하고 있다.
B. Parameter Estimation Under Sparsity
: linear/polynomial SVM 모델이 sparse 문제에서 적용될 수 없는 이유를 설명한다.
active user에 해당하는 u번째와 active item에 해당하는 i번째 성분만 non-zero인, 즉 2개의 성분을 제외하고 모두 0인 매우 sparse한 feature vectors를 가정한다.
1) Linear kernel
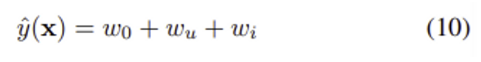
j = u 혹은 j = i인 경우에만 x_j = 1이므로 (active user u와 active item i 성분만 non-zero) predictor 추정식은 매우 간단하다. 하지만 그만큼 예측이 정교하지 못하다.
2) Polynomial kernel
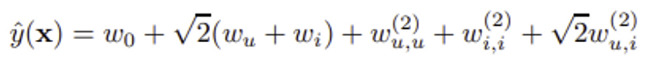
users와 items간 interaction 항들이 추가된다. m(x)=2인 이 예시에서 predictor 추정식은 위와 같다.
- 일반적인 협력 필터링(CF) 문제의 경우 각각의 interaction w(2)_u,i에 대한 정보를 얻을 수 있는 data (u,i)가 train set에 최대 1개 있고, test set에 존재하는 (u’, i’)에 대한 data는 train set에 보통 존재하지 않는다. 즉 train set에 interaction과 관련된 data가 많아야 1개 존재하거나 아예 존재하지 않는다.
- 따라서 모든 테스트 사례(u,i)에 대한 상호 작용 매개 변수 w(2)_u,i에 대한 최대 margin 해가 0이 되고, polynomial SVM의 interaction 항들은 test case를 예측하는데 사용할 수 없게 된다. 즉 polynomial SVM은 user와 item biases에만 의존하게 되고 linear SVM보다 더 나은 추정을 제공할 수 없다.
➡️ SVM에서 (i, j)의 interaction parameter w(2)i,j를 추정하기 위해선 x_i도 non-zero이고 x_j도 non-zero인 data가 학습 데이터 D에 충분히 존재해야 한다. 따라서 (i, j)에 대한 data가 충분히 존재하지 않는 경우 SVM은 좋은 예측을 할 수 없게 된다. 위에서 예로 든 CF뿐만 아니라 데이터가 hugely sparse한 어느 상태에서든SVM은 고차원 interaction을 제대로 추정하지 못하게 된다.
C. Summary
📌 `dense parametrization` 을 사용하는 SVM은 interaction 정보에 대한 직접적인 data를 활용해 interaction을 모델화한다. 이 원리는 아래와 같은 SVM과 FM의 차이를 야기한다.
- FM과 달리, data가 충분하지 않은 high sparsity에서 변수 사이의 상호작용을 제대로 추정할 수 없다.
- 즉각적인 학습이 가능한 FM과 달리, non-linear SVM은 dual(쌍대 문제)를 통해 학습한다.
- 모델 방정식이 train data에서 독립적인 FM과 달리, SVM의 모델 방정식은 train data에 의존적이다.
5. CONCLUSION AND FUTURE WORK
[논문 내용 요약]
- factorization machines, FM의 원리
- SVM에 비해 뛰어난 점
- huge sparsity인 데이터에서도 parameters를 추정할 수 있다.
- model parameters의 수와 방정식의 계산 복잡도가 linear하다.
- 즉각적인 최적화가 가능하다. - factorization models에 비해 뛰어난 점
- general predictor이다.
- input feature vector만 적절히 맞추어준다면 손쉽게 전문화된 factorization models을 모방할 수 있다.
'deep daiv. > 추천시스템 스터디' 카테고리의 다른 글
| [추천시스템 논문 리뷰] 4주차 : Loss function (0) | 2023.08.26 |
|---|---|
| [추천시스템 논문 리뷰] 3주차 : 경사하강법 / SGD (0) | 2023.08.24 |
| [추천시스템 논문 리뷰] 3주차 : SVM (0) | 2023.08.23 |
| [추천시스템 학습] 1주차 : 협업 필터링 (0) | 2023.08.07 |
| [추천시스템 학습] 1주차 : 콘텐츠 기반 필터링 (0) | 2023.08.01 |




